Предмет: Геометрия,
автор: Murvef
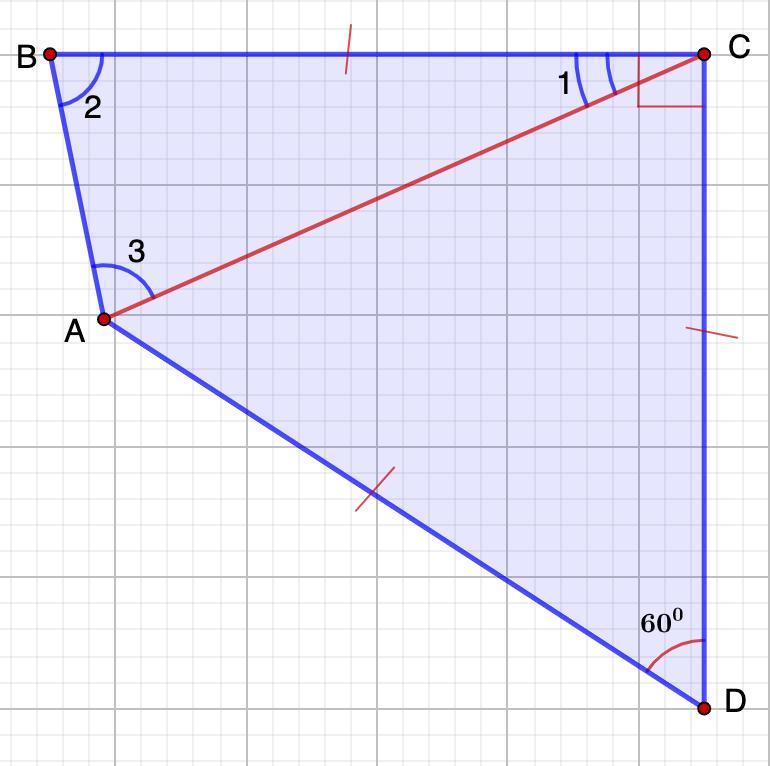
Три стороны выпуклого четырёхугольника равны, а два его угла между ними равны 60° и 90°. Найдите два других угла этого четырёхугольника
Ответы
Автор ответа:
33
Ответ:
Два других угла этого четырёхугольника равны 75° и 135°.
Объяснение:
Требуется найти два других угла этого четырёхугольника.
Дано: ABCD - четырехугольник.
∠С = 90°; ∠D = 60°;
BC = CD = AD
Найти: ∠А и ∠В.
Решение:
Соединим А и С.
1. Рассмотрим ΔACD.
CD = AD (условие)
⇒ ΔACD - равнобедренный.
- Углы при основании равнобедренного треугольника равны.
⇒ ∠DAC = ∠DCA
- Сумма углов треугольника равна 180°.
⇒ ∠DAC = ∠DCA = (180° - ∠D) : 2 = (180° - 60°) : 2 = 60°
- Если в треугольнике все углы равны 60°, то этот треугольник равносторонний.
⇒ CD = AD = AC.
2. Рассмотрим ΔАВС.
ВС = CD (условие)
АС = CD (п.1)
⇒ ВС = АС
ΔАВС - равнобедренный.
∠1 = ∠С - ∠ACD = 90° - 60° = 30°
∠2 = ∠3 = (180° - ∠1) : 2 = (180° - 30°) : 2 = 75° (углы при основании равнобедренного треугольника)
3. Найдем ∠А и ∠В.
∠В = ∠2 = 75°
∠А = ∠1 + ∠CAD = 75° + 60° = 135°
Два других угла этого четырёхугольника равны 75° и 135°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: эля614
Предмет: Русский язык,
автор: Lerenok4
Предмет: Русский язык,
автор: hoper123
Предмет: Геометрия,
автор: brabus613
Предмет: Қазақ тiлi,
автор: aibek2011