Предмет: Алгебра,
автор: Аноним
Помогите умоляю(((((((
Приложения:
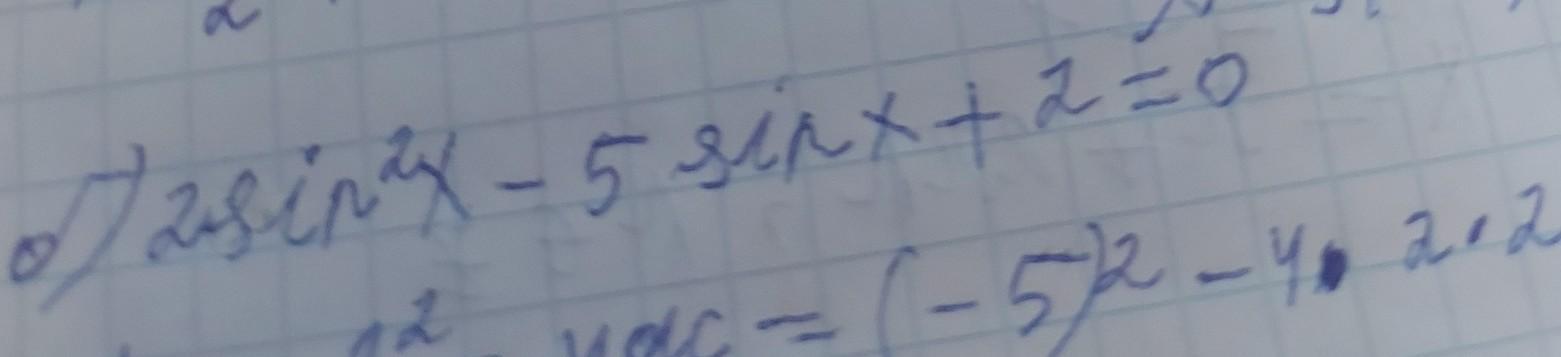
Ответы
Автор ответа:
0
Ответ:
30
Объяснение:
2sin²x-5sinx+2=0
Пусть sinx=t, тогда получим:
2t²-5t+2=0
D=b²-4ac=25-16=9
t1=(5+3)/4=2
t2=(5-3)/4=0,5
Произведём обратную замену:
sinx=2;0,5 (Но sinx=2 – не подходит, т.к. -1<sin<1)
Отсюда: sinx=0,5
x=30° ( т.к. sin30°=1/2=0,5)
Автор ответа:
0
Ответ:
Замена:
Похожие вопросы
Предмет: Русский язык,
автор: yuliya167
Предмет: Окружающий мир,
автор: Arseny2000
Предмет: Английский язык,
автор: славиккккк
Предмет: Математика,
автор: Vova2565
Предмет: Физика,
автор: nikitkamoroz21