Предмет: Алгебра,
автор: suigemar86
NNNLLL54 помогите пж :)
Приложения:
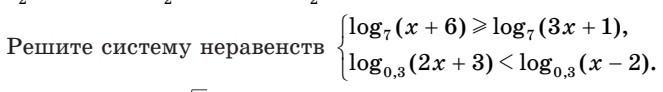
suigemar86:
Добрый день, Universalka!
Добрый день . Я решила , так как я первый заместитель NNNLLL54 :))
Спасибо :)
Простите что не поставил вам лучший
Ничего страшного
Ответы
Автор ответа:
3
ответ х€(2,5/2]
решение на фотографии
Приложения:

Спасибо
Автор ответа:
3
Окончательно : x > 2
С учётом ОДЗ окончательный ответ :
Спасибо!
Universalka простите ваш ответ объективный и понятен. Я хочу лучший ответ поставить новичку.
Чтобы у него уже был хотя бы один лучший ответ
Простите я бы вам поставил
Незачто
Не переживайте, Вы всё сделали правильно .
Похожие вопросы
Предмет: Русский язык,
автор: violetta206
Предмет: Русский язык,
автор: ratkovaAnna56
Предмет: Английский язык,
автор: gessdolan
Предмет: Математика,
автор: kamarik1989
Предмет: Українська мова,
автор: goovi001