Предмет: Алгебра,
автор: tawmuhamedovam
Способ алгебраического сложения решить систему уравнений (79-82)
Приложения:
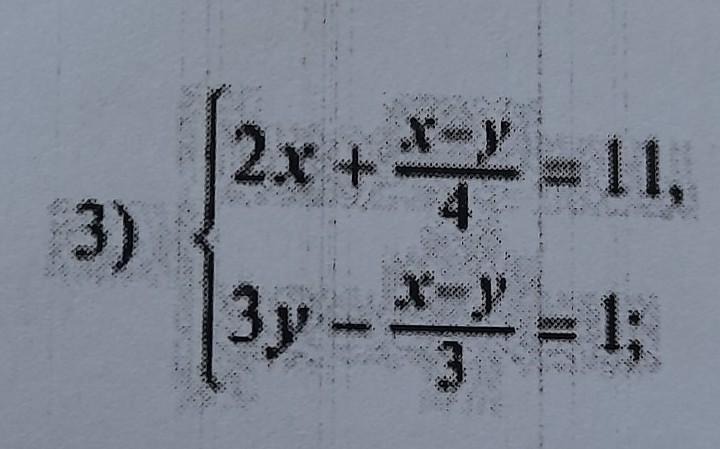
Ответы
Автор ответа:
2
Ответ:
x =
y =
Объяснение:
⇒
⇒ +
89y=71
y=
Похожие вопросы
Предмет: Русский язык,
автор: sika1
Предмет: Русский язык,
автор: polinacat2004
Предмет: Английский язык,
автор: Nanami2312
Предмет: Биология,
автор: aleschaboitan
Предмет: Алгебра,
автор: fsry6