Помогите решить задачи, срочно надо
Ответы
Ответ:
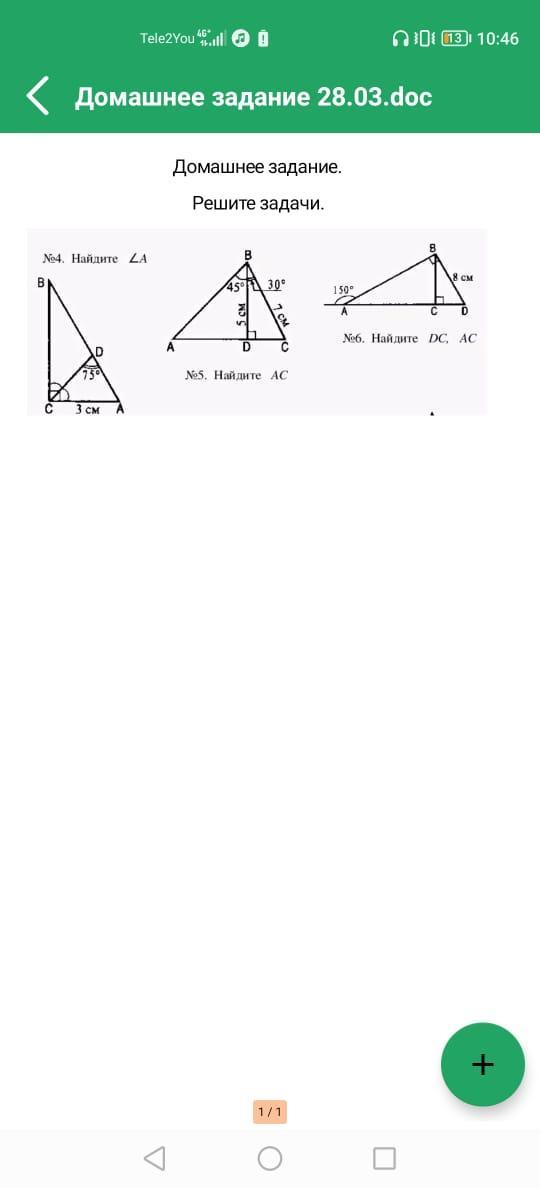
4) На рисунке отмечено, что ∠СДА=75° , ∠С=90° , ∠ВСД=∠АСД , значит СД - биссектриса и ∠ВСД=∠АСД=90°:2=45° .
Сумма углов в треугольнике = 180° . Поэтому в ΔАСД сумма
∠АСД+∠СДА+∠САД=180° , 45°+75°+∠САД+=180° ,
∠САД=180°-45°-75°=60°
∠А=∠САД=60°
Ответ: ∠А=60° .
5) ΔАВС , ВД ⊥ АС , ВД=5 см , ∠АВД=45° , ∠СВД=30° , ВС=7 см .
ΔВСД - прямоугольный , напротив угла в 30° лежит катет, равный половине гипотенузы, поэтому СД=ВС:2=7:2=3,5 (см) .
ΔАВД - прямоугольный с острым углом в 45° , значит второй острый угол равен тоже 45° и ΔАВД имеет два равных угла, значит он равнобедренный, поэтому АД=ВД=5 см .
АС=АД+СД=5 см+3,5 см=8,5 см .
Ответ: АС=8,5 см .
6) ΔАВД , ∠В=90° , ВС ⊥ АД , ВД=8 см , внешний угол Δ при вершине А = 150°
∠ВАС=180°-150°=30° , ∠Д=180°-30°-90°=60°
ΔВСД - прямоугольный , ∠Д=60° , значит ∠СВД=90°-60°=30° (сумма острых углов в прямоугольном треугольнике равна 90°) .
ДС - катет, лежащий против угла в 30°, значит он равен половине гипотенузы, то есть ДС=ВД:2=8:2=4 (см) .
По теореме Пифагора: ВД²=ВС²+ДС² ⇒
ВС=√(ВД²-ДС²)=√(64-16)=√48=4√3 (см)
Рассм. ΔАВС , ∠АСВ=90° , ∠ВАС=30° .
Против угла в 30° лежит катет ВС, он равен половине АВ , значит
АВ=2*ВС=2*4√3=8√3 (см)
По теореме Пифагора АВ²=АС²+ВС² ⇒ АС²=АВ²-ВС² ,
АС²=64*3-16*3=144 , АС=12 (см)
Ответ: АС=12 см , ДС=4 см .