Question

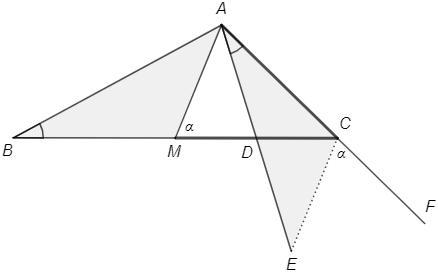
В треугольнике ABC выполняется равенство BC = 2AC. На стороне BC выбрана такая точка D, что ∠CAD = ∠CBA. Прямая AD пересекает биссектрису внешнего угла C в точке E. Докажите, что AE = AB.

Answer 1

M - середина BC

BM=MC=AC (по условию)

△ACM - равнобедренный, углы при основании равны, ∠CMA=∠CAM=a

Внешний угол треугольника равен сумме внутренних, не смежных с ним.

∠MCF=2a => ∠FCE=∠MCF/2=a

=> ∠BMA=∠ACE (смежные с равными)

△BMA=△ACE (по стороне и прилежащим углам) => AB=AE