Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
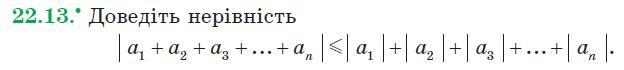
Ответы
Автор ответа:
2
Ответ:
Для того, чтобы доказать, что
|a₁ + a₂ + a₃ + . . . + aₙ| = |a₁| + |a₂| + |a₃| + . . . + |aₙ|
используем метод математической индукции
1. покажем, что утверждение верно для n = 1:
n = 1;
|a₁| = |a₁|
А так как |a₁| = |a₁|, то утверждение верно для n = 1
2. предположим, что утверждение верно для любого n = k:
n = k;
- пусть верно
3. покажем, что при допущении 2. утверждение верно и для n = k + 1:
Так как мы предполагаем, что верно
то для n = k + 1 необходимо доказать, что , а это верно так как модуль числа больше или равен чем само число, то есть методом математической индукции исходное утверждение доказано, то есть
|a₁ + a₂ + a₃ + . . . + aₙ| = |a₁| + |a₂| + |a₃| + . . . + |aₙ|
Ч.Т.Д
Приложения:


Похожие вопросы
Предмет: Русский язык,
автор: ерген3
Предмет: Русский язык,
автор: арианна1004
Предмет: Русский язык,
автор: Аноним
Предмет: Биология,
автор: Water555
Предмет: Русский язык,
автор: glyshenkovaleria