Задание приложено...
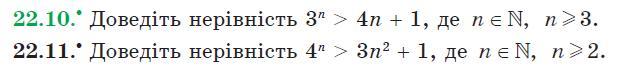
Ответы
22.10
Применим метод математической индукции
Шаг 1 n=3 3³>4*3+1 неравенство выполняется
Шаг 2 n=k
Предполагаем, что неравенство имеет место при n=k.
3^k>4k+1 (1)
Шаг 3 покажем , что неравенство имеет место при n=k+1
3^(k+1)=3*3^k 4(k+1)+1=4k+4+1
заменим 4k+1 на заведомо большее
найдем разницу
3*3^k - (4(k+1)+1)>3*3^k-3^k-4=3^k(3-1)-4=
=2*3^k-2*2=2*(3^k-2)>0
неравенство доказано
22.11
Применим метод математической индукции
Шаг 1 n=2 4²>3*2²+1 неравенство выполняется
Шаг 2 n=k
Предполагаем, что неравенство имеет место при n=k.
4^k>3k²+1 (2)
Шаг 3 покажем , что неравенство имеет место при n=k+1
4^(k+1)=4*4^k 3(k+1)^2+1=3k^2+3+1+6k=(3k^2+1)+3+6k
заменим (3k^2+1) на заведомо большее
найдем разницу
4*4^k - ((3k^2+1)+3+6k)=4*4^k-4^k-6k-3=4^k(4-1)-3-6k=
=3*4^k-6k-3=3*(4^k-2k-1)>0
k>=2 положим k=2 4^2-2*2-1>0
неравенство доказано
Ответ:
22.10
- пусть верно
------------------------------------------------------
Необходимо доказать:
По индуктивному предположению
То, есть нужно доказать, что
Прологарифмируем по основанию 3 неравенство ( по свойству показательной функции)
Оценим значение логарифма
А минимальное по условию равно 3, то есть неравенство выполнено.
Так как сумма двух положительных чисел больше нуля, то утверждение для верно.
Так как , то неравенство
доказано методом математической индукции.
22.11
- пусть верно
------------------------------------------------------
Необходимо доказать:
По индуктивному предположению
То, есть нужно доказать, что
- пусть верно
------------------------------------------------------
Необходимо доказать:
По индуктивному предположению
То, есть нужно доказать, что
Прологарифмируем по основанию 4 неравенство ( по свойству показательной функции)
Оценим значение логарифма
А минимальное по условию равно 2, то есть неравенство выполнено.
Так как сумма двух положительных чисел больше нуля, то утверждение для верно.
Так как , то неравенство
доказано методом математической индукции.
Тогда так как и
, а сумма двух положительных чисел есть положительное число, то утверждение верно для
, следовательно исходное неравенство тоже верно и методом математической индукции доказано, что

