Предмет: Алгебра,
автор: 56fj
вычислить інтеграл, помогите ПОЖАЛУЙСТА
Приложения:
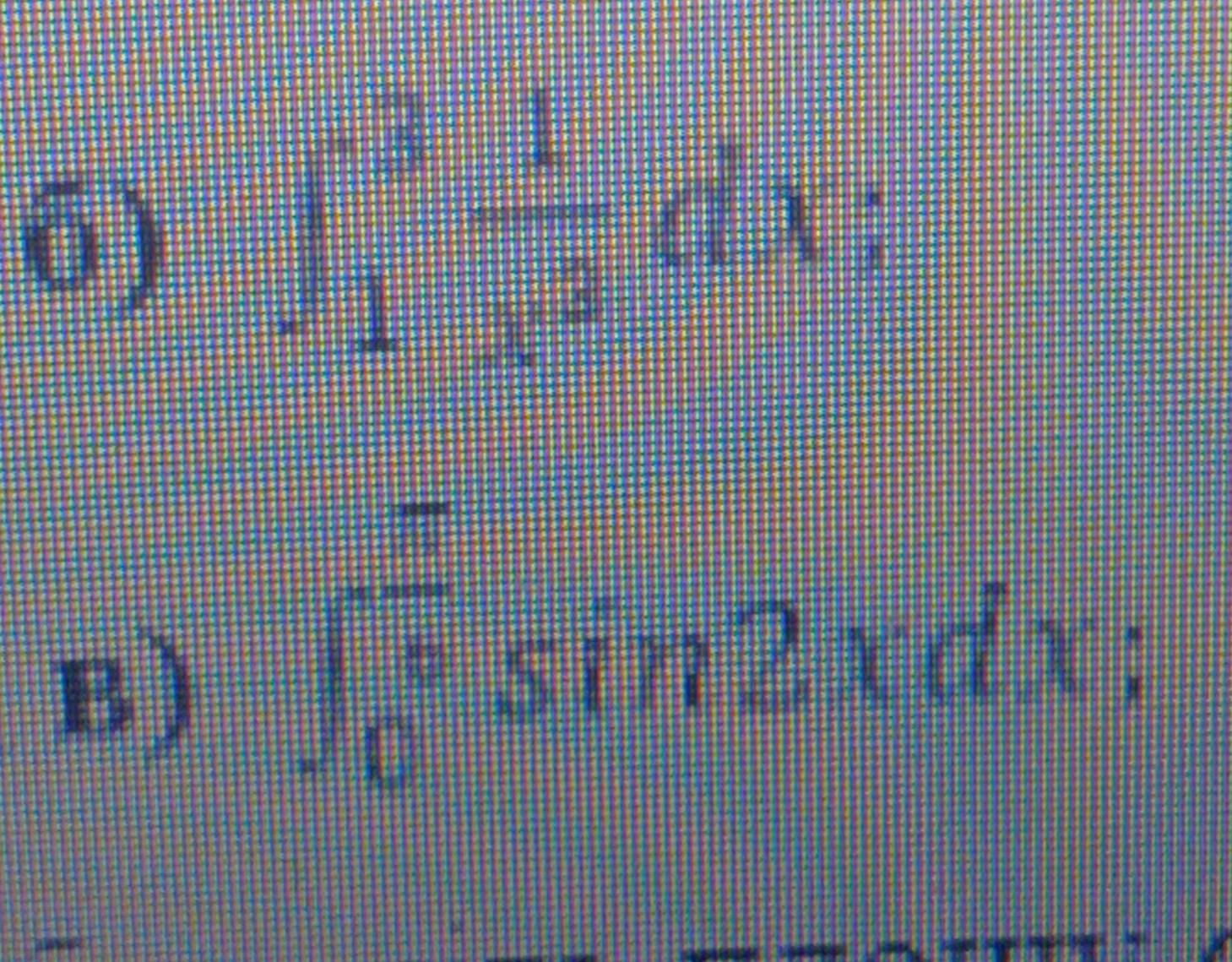
Ответы
Автор ответа:
0
Ответ:
Применяем формулу Ньютона-Лейбница для вычисления определённого интеграла .
Похожие вопросы
Предмет: Русский язык,
автор: Praskoviatitova
Предмет: Английский язык,
автор: 1246898dashs
Предмет: Английский язык,
автор: 17048327
Предмет: Литература,
автор: moool11
Предмет: Қазақ тiлi,
автор: lera119416