Предмет: Математика,
автор: microclock1337
решите пожалуйста два примера 75 баллов!
Приложения:
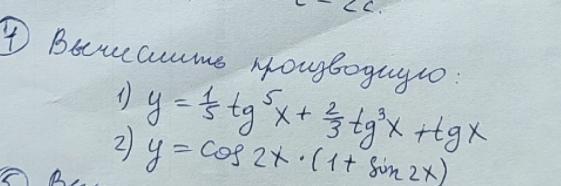
Ответы
Автор ответа:
0
Пошаговое объяснение:
1)y'=(tg⁵x/5+2tg³x/3+tgx)'=
(5/5)(tg⁴(x))*(1/cos²(x))+(2/3)*(3tg²(x))(1/cos²(x))+1/cos²(x))=
(1/(cos²(x))*(tg⁴(x)+2tg²(x)+1)=(1/(cos²(x))*(tg²(x)+1)²=1/(cos²(x))*(1/(cos²x))²=1/cos⁶x
2)y'=
(cos(2t))'*(1+sin(2t))+(1+sin(2t))'*(cos(2t))=-2(sin(2t))*(1+sin(2t))+(cos(2t))(2cos(2t))=
-2(sin(2t))-2sin²(2t)+2cos²(2t)=2(cos²(2t)-sin²t)-2sin2t=2(cos(4t))-2(sin(2t))
Автор ответа:
1
Ответ:
Применяем правила дифференцирования и таблицу производных .
Похожие вопросы
Предмет: Русский язык,
автор: еее95
Предмет: Другие предметы,
автор: блэйдон
Предмет: Русский язык,
автор: 201227
Предмет: Литература,
автор: masha342320
Предмет: Математика,
автор: Аноним