Question

Помогите пжлста с построением и решением ;(​

Answer 1

УСЛОВИЕ: В правильной шестиугольной пирамиде SABCDEF сторона основания равна 6, а боковое ребро 10.

1) Докажите, что SA⊥BF; будет ли SA⊥DE?

2)вычислите: а) высоту пирамиды; б) угол между SA и плоскостью основания; в) площадь сечения, проведенного через середину высоты перпендикулярно высоте; г) Угол между ребром SA и SE; д) угол между плоскостями ABS и EDC

РЕШЕНИЕ:

1. Вычислите высоту пирамиды. SO = ?

  Рассмотрим ΔSOB (∠O=90°)

  OB=6 ; SB=15 тогда по теореме Пифагора $\displaystyle SO = \sqrt{10^2-6^2} =\sqrt{100-36} =\sqrt{64} =8$

Ответ: SO=8 - высота

2. Докажите, что SA⊥BF

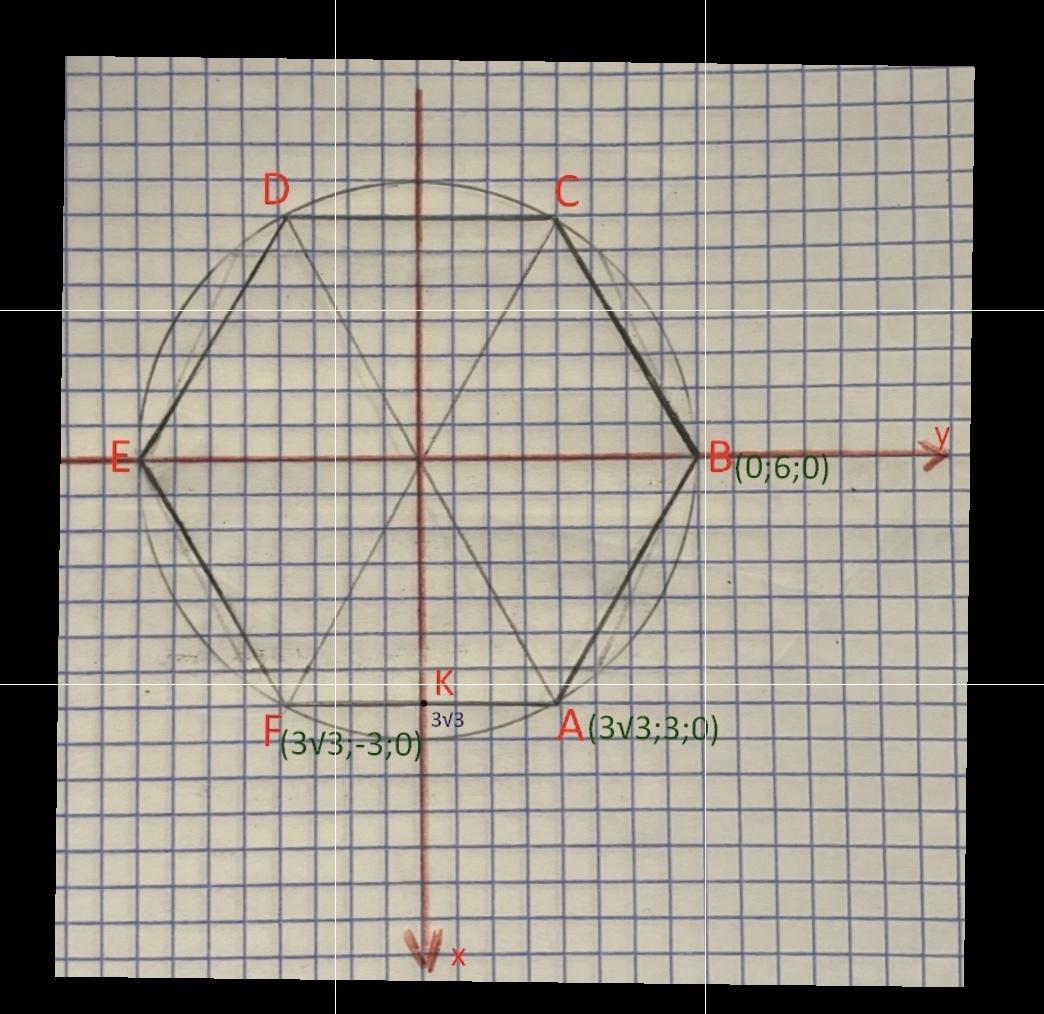
   S(0;0;8) ; А(3√3;3;0)  $\large \overrightarrow {\rm SA}\{3\sqrt{3} ; 3;-8\}$

   В(0;6;0) ; F(3√3; -3;0) $\large \overrightarrow {\rm BF}\{3\sqrt{3} ;-9;0\}$

$\large \overrightarrow {\rm SA} * \overrightarrow {\rm BF}=3\sqrt{3} *3\sqrt{3} +3*(-9)+(-8)*0=27-27=0$

Если скалярное произведение = 0, то векторы перпендикулярны, значит SA⊥BF (ч.т.д)

3. Будет ли SA⊥DE?

   $\large \overrightarrow {\rm SA}\{3\sqrt{3} ;3;-8\}$

   D(-3√3;-3;0) ; Е(0;-6;0) ⇒ $\large \overrightarrow {\rm DE}\{3\sqrt{3} ;-3;0\}$

   $\large \overrightarrow {\rm SA}*\overrightarrow {\rm DS} = -3\sqrt{3} *3\sqrt{3} -3*3+(0)*0=27-9 =18 \neq 0$ , если скалярное произведение не равно нулю, то векторы не перпендикулярны значит и прямые, содержащие векторы также не перпендикулярны.

Ответ: SA не ⊥ DE

4. Найти угол между SA и плоскостью основания, т.е ∠SAO

  Рассмотрим ΔSOA: ∠О=90°, ОА=6, SA=10

  cos∠SAO=ОА/SA=6/10=0,6

   ∠SOA=arccos0,6  -ответ

5. Вычислить площадь сечения, проведенного через середину высоты перпендикулярно высоте. Sсеч. = SА₁В₁С₁D₁E₁F₁

1)  $\displaystyle Socn. = 6 * \frac{a^2\sqrt{3} }{4} =\frac{6*36*\sqrt{3} }{4} =54\sqrt{3}$

2) Сечение будет правильный шестиугольник подобный основанию с R=2

(SABCDEF)/Sсеч. = 2²

(54√3)/Scеч. = 4

Sсеч. = (54√3)/4

Sсеч. = 13,5√3   -ответ

6. Найдите угол между ребром SA и SE.

 Рассмотрим ΔASE: SA=10, SE=10, EA=a√3=6√3

по теореме косинусов:

EA²=SA²+EA²-2SA*SE*cos∠S

(6√3)²=10²+10²-2*10*10*cos∠S

108=100+100-200cos∠S

200*cos∠S=92

cos∠S=92/200=46/100=0,46

cos∠S=0,46 ⇒ ∠S=arccos0,46 -ответ

7. Найдите угол между плоскостями ABS и EDC - это угол между гранью ABS и основанием, т.е ∠SKO, т.е SK⊥AB (К - середина АВ)

ОК⊥AD ( ОК - медиана в ΔАОВ)

∠SKO - линейный угол двугранного угла между гранями ABS и EDS.

Рассмотрим ΔSOK: SO =8, OK=3√3

tg∠SKO=SO/OK=8/(3√3)=(8√3)/9

∠SKO=arctg(8√3)/9. -ответ

Удачи!