Предмет: Геометрия,
автор: burbiloviktoria39
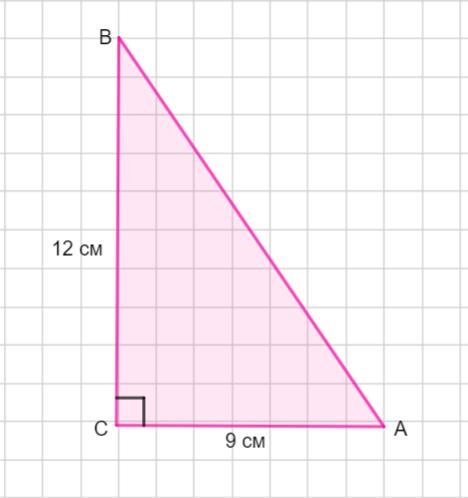
За двома сторонами прямокутного трикутника АВС (кут С дорівнює 90градусів ) знайдіть його третю сторону та гострі кути: АС = 9 см; ВС = 12 см. Терміново, і малюнок
Ответы
Автор ответа:
2
Ответ:
Гипотенуза равна 15 см, а острые углы приближенно
равны 53° и 37°.
Объяснение:
По условию задан прямоугольный Δ АВС, так как ∠С=90°.
Катеты этого прямоугольного треугольника АС=9 см, ВС=12 см.
Найдем гипотенузу прямоугольного треугольника по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Значит, гипотенуза равна АВ= 15 см .
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе
Тогда ∠A .
Найдем градусную меру угла А по таблицам Брадиса.
∠А≈53°.
Так как сумма острых углов прямоугольного треугольника равна 90°, то ∠В= 90°- 53°=37°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: lerak08901
Предмет: Русский язык,
автор: dfdddcg
Предмет: Английский язык,
автор: Nikita35JR
Предмет: Қазақ тiлi,
автор: naletovadianazp92k8r
Предмет: История,
автор: Лёшенька555