Question

На гипотенузе АВ прямоугольного треугольника АВС отмечена точка К, а на
отрезке СК – точка N так, что AK :KB = KN:CN =1:2. Найдите площадь тре-
угольника BCN, если AC = 9, BC =16.

Answer 1

Ответ:

Площадь треугольника BCN равна 32 ед.²

Объяснение:

Требуется найти площадь треугольника BCN.

Дано: ΔАВС - прямоугольный.

К ∈ АВ; N ∈ CK;

AK : KB = KN : CN = 1 : 2

AC = 9; BC =16.

Найти: S (BCN)

Решение:

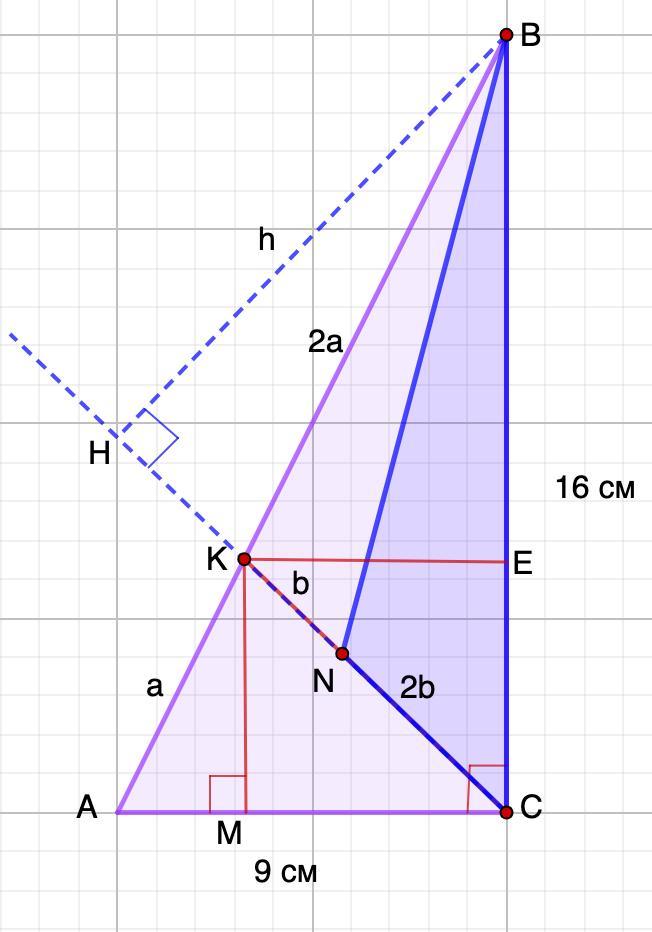
Дополнительное построение:

КМ ⊥ АС; КЕ || АС.

Продолжим СК и из точки В опустим перпендикуляр ВН.

1. AK : KB = KN : CN = 1 : 2

Пусть АК = а, тогда КВ = 2а.

Пусть KN = b, тогда NC = 2b.

2. Найдем площадь ΔАВС.

• Площадь прямоугольного треугольника равна половине произедения катетов.

$\displaystyle S(ABC) = \frac{1}{2}AC\cdot{BC}=\frac{1}{2} \cdot9\cdot16=72$

3. Рассмотрим ΔАКМ и ΔАВС.

КМ ⊥ АС (построение)

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ КМ || ВС

• Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.

⇒ΔАКМ ~ ΔАВС

Запишем отношения сходственных сторон:

$\displaystyle \frac{AK}{AB} =\frac{MK}{BC} =\frac{a}{3a}=\frac{1}{3} \\\\MK=\frac{BC}{3}=\frac{16}{3}$

4. Найдем площадь ΔАКС.

• Площадь треугольника равна половине произведения высоты на сторону, к которой она проведена.

$\displaystyle S(AKC) = \frac{1}{2}\cdot{AC} \cdot{KM = \frac{1}{2} }\cdot9\cdot\frac{16}{3}=24$

5. Найдем площадь ΔКВС.

$\displaystyle S(KBC) = S(ABC)-S(AKC) = 72-24 = 48$

6. Рассмотрим ΔКВN и ΔNBC.

Пусть BН = h - высота ΔКВN и ΔNBC.

$\displaystyle S(KBN)=\frac{bh}{2}\\\\S(NBC)=\frac{2bh}{2}=bh\\ \\ S(KBN) : S(NBC)=1:2\\\\\Rightarrow S(NBC)=S(KBC):3\cdot2 = 48:3\cdot2=32$

Площадь треугольника BCN равна 32 ед.²