Предмет: Геометрия,
автор: anna23podkalyk
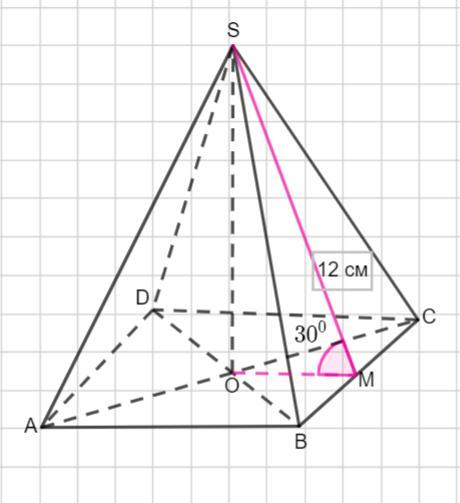
Апофема правильної чотирикутної піраміди дорівнює 12 см і утворює з площиною основи кут 30 градусів. Знайдіть об’єм піраміди
zmeura1204:
Н=12*2=24; а/2=12√3; а=24√3. V=(24√3)²*24/3=13824
Ответы
Автор ответа:
1
Ответ:
Объем пирамиды равен 864 см ³.
Объяснение:
Пусть дана правильная четырехугольная пирамида SABCD .
Апофема SM= 12 см. ∠ SMO= 30°.
SO- высота пирамиды. Тогда ΔSОM- прямоугольный.
По свойству катета, лежащего напротив угла в 30°, катет SO равен половине гипотенузы SM.
Тогда высота пирамиды равна 6 см.
Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Тогда сторона основания пирамиды
Основанием данной пирамиды является квадрат со стороной
12√3 см. Найдем площадь основания пирамиды, то есть площадь квадрата
см².
Найдем объем пирамиды
Объем пирамиды равен 864 см ³.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sasha1255
Предмет: Другие предметы,
автор: Набиева1
Предмет: Русский язык,
автор: Нет5дз
Предмет: Физика,
автор: masha2101mailru2001
Предмет: Другие предметы,
автор: vlad83377