Предмет: Алгебра,
автор: sinus348
Даю 25 баллов, 13.12 задание. Срочно!
Приложения:
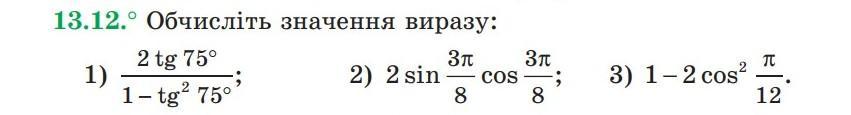
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: DEMON6661yf
Предмет: Русский язык,
автор: lityr
Предмет: Английский язык,
автор: SuperROPE
Предмет: Математика,
автор: ggadgziragimov88
Предмет: Алгебра,
автор: vladimirkaush