помогите пожалуйста
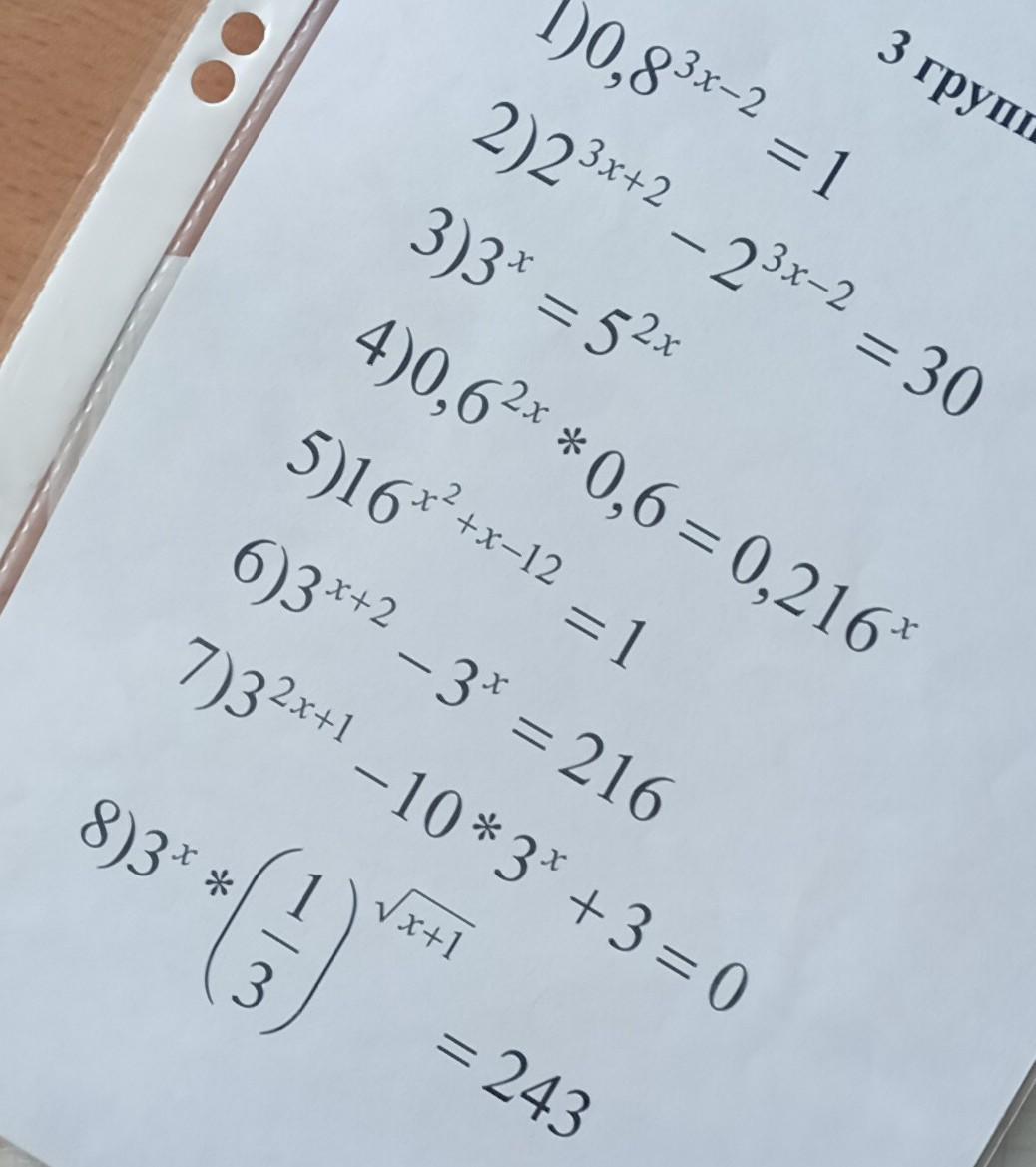
Ответы
Пошаговое объяснение:
1) 0,8^(3x-2) = 1
0,8^(3x-2) = 0,8^0
3x-2 = 0
x = 2/3;
2) 2^(3x+2) - 2^(3x-2) = 30
2^(3x-2) * (2^4 - 1) = 30
2^(3x-2) = 2
3x - 2 = 1
x = 1;
3) 3^x = 5^(2x)
Логарифмируем по основанию 3
log3 (3^x) = log3 (5^(2x))
x = 2x * log3 (5)
x(1 - 2log3 (5)) = 0
x = 0;
4) 0,6^(2x) * 0,6 = 0,216^x
0,6^(2x+1) = 0,6^(3x)
2x + 1 = 3x
x = 1;
5) 16^(x^2 + x - 12) = 1
16^(x^2 + x - 12) = 16^0
x^2 + x - 12 = 0
по т. Виета x1 = -4; x2 = 3;
6) 3^(x+2) - 3^x = 216
3^x * (3^2 - 1) = 216
3^x = 27
3^x = 3^3
x = 3;
7) 3^(2x+1) - 10*3^x + 3 = 0
Заменим 3^x = t; 3^(2x+1) = 3^(2x) * 3
3 * t^2 - 10t + 3 = 0 => D = 100 - 4*3*3 = 64 = 8^2
t1 = (10 + 8)/(2*3) = 3
t2 = (10 -8)/(2*3) = 1/3
Обратная замена
3^x = 3 => x1 = 1
3^x = 1/3 => x2 = -1;
8) 3^x * (1/3)^(sqrt(x+1)) = 243 ОДЗ: x+1 >= 0 => x >= -1
3^x * 3^(-(sqrt(x+1))) = 243
3^(x -(sqrt(x+1))) = 3^5
x - sqrt(x+1) = 5
x - 5 = sqrt(x+1) Возводим обе части в квадрат
x^2 - 10x + 25 = x + 1
x^2 - 11x + 24 = 0
по т, Виета x1 = 3; x2 = 8; корни подходят по ОДЗ.
Проверка:
1. 3^3 * (1/3)^(sqrt(3+1)) = 243
27*(1/9) = 243 неверно
2. 3^8 * (1/3)^(sqrt(8+1)) = 243
3^8 / 3^(-3) = 243 верно
Ответ: х = 8