Предмет: Математика,
автор: hhssbb228007
Вычислите площадь фигуры, ограниченной кривыми. Сделайте чертеж.
y=x^2-3x-1, y=-x^2=2
Приложения:
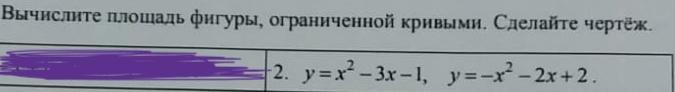
Ответы
Автор ответа:
1
Ответ:
Площадь фигуры равна кв. ед.
Пошаговое объяснение:
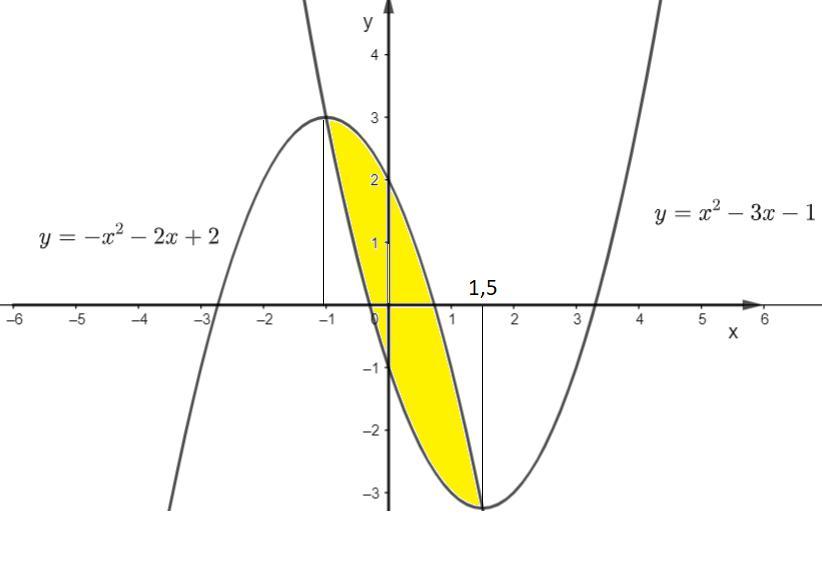
Выполним рисунок. Графиком функции является парабола, ветви которой направлены вверх. Найдем координаты вершины параболы
Определим еще несколько точек, по которым построим параболу
(0; -1) (1; -3), ( 2; -3) и (3; -1)
Графиком функции является парабола, ветви которой направлены вниз . Найдем координаты вершины параболы
( -3; -1 )(-2; 2 ) (0; 2) и ( 1; -1) - точки лежащие на этой параболе. Выполним рисунок и покажем фигуру, ограниченную данными параболами.
Найдем абсциссы точек пересечения, решив уравнение:
Тогда найдем площадь фигуры, ограниченной параболами.
Значит, площадь фигуры равна кв. ед.
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: 909050
Предмет: Қазақ тiлi,
автор: ainur19881988gmailru
Предмет: Русский язык,
автор: drol234
Предмет: Русский язык,
автор: Poliika
Предмет: Английский язык,
автор: MrFoxestry