Предмет: Алгебра,
автор: arslan051005
ПОЖАЛУЙСТААААА!!!
все на фото 2 задания
Приложения:
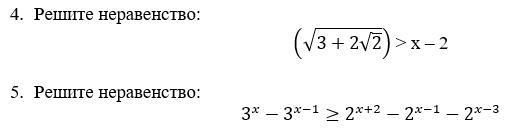
Ответы
Автор ответа:
1
4)
правая часть положительное число
а) если x-2 ≤0, т.е. x≤2
то левая часть не будет положительным числом. И тогда данное неравенство будет справедливым
значит при x∈(-∞;2]
б) если х-2>0. т.е. x>2 тогда левая часть положительное число
решаем неравенство
значит x∈(2; 2+√(3+2√2))
общий ответ: (-∞;2+√(3+2√2))
5)
(т.к. основание 3/2>1 то при переходе к показателям знак неравенства не меняется)
Похожие вопросы
Предмет: Другие предметы,
автор: Pervoklasniza
Предмет: Українська мова,
автор: яна1195
Предмет: Английский язык,
автор: Lilya345
Предмет: Литература,
автор: RozieDeMusic
Предмет: Математика,
автор: marya18hvid