Question

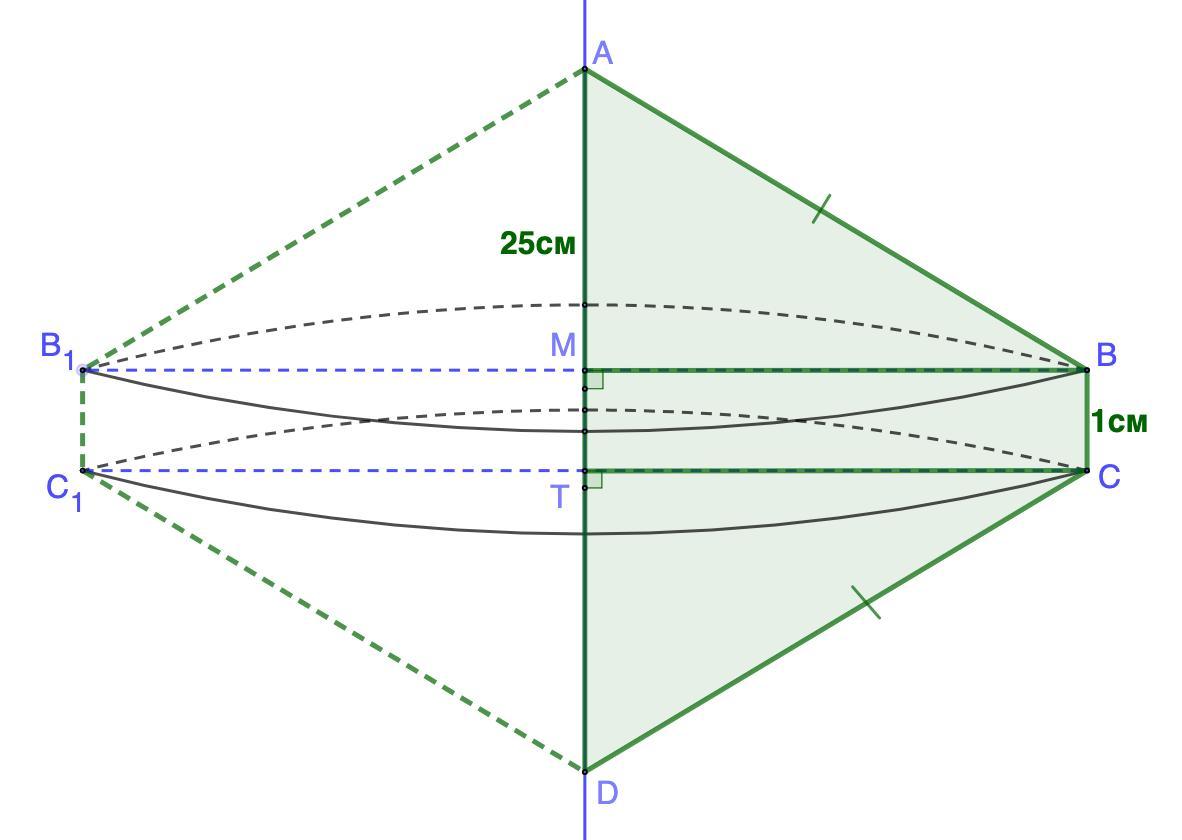
100 баллов : Рівнобічну трапецію з основами 1 см і 25 см обертають навколо прямої, що містить її більшу основу. Знайдіть об’єм отриманого тіла, якщо відомо, що в дану трапецію можна вписати коло.

Answer 1

Ответ:

Объем полученного тела равен 225π см³.

Объяснение:

Равнобедренную трапецию с основаниями 1 см и 25 см вращают вокруг прямой, содержащей его большее основание. Найдите объем полученного тела, если известно, что в данную трапецию можно вписать окружность.

Дано: ABCD - равнобедренная трапеция,

вращается вокруг AD.

ВС = 1 см; AD = 25 см.

В трапецию можно вписать окружность.

Найти: объем тела вращения.

Решение:

При вращении получим два конуса с образующими АВ и CD и цилиндра с образующей ВС.

Трапеция равнобедренная, поэтому конусы будут равные.

1. Найдем объем цилиндра.

Объем цилиндра равен:

$\displaystyle \boxed {V=\pi r^2h}$, где r - радиус основания, h - высота (образующая)

h = BC = 1 см.

r = МВ - высота трапеции ABCD

• В равнобедренной трапеции высота, опущенная из вершины тупого угла на большее основание, делит его на части, меньшая из которых равна полуразности оснований.

⇒ АМ = (AD - BC) : 2 = (25 - 1) : 2 = 12 (см)

• Если в трапецию можно вписать окружность, то суммы длин ее противоположных сторон равны.

АВ + CD = BC + AD = (1 + 25) = 26 (см)

⇒ АВ = CD = 26 : 2 = 13 (см)

Рассмотрим ΔАВМ - прямоугольный.

По теореме Пифагора найдем ВМ:

ВМ² = АВ² - АМ² = 13² - 12² = 169 - 144 = 25

ВМ = √25 = 5 (см)

Vц = π · ВМ² · ВС = π · 25 · 1 = 25π (см³)

2. Найдем объем конуса.

Объем конуса равен:

$\displaystyle \boxed {V=\frac{1}{3} \pi r^2h}$ , где r - радиус основания, h - высота.

r = BM = 5см

h = AM = 12 см

$\displaystyle V_k=\frac{1}{3}\pi \cdot5^2\cdot12=100\pi \;_{(CM^3)}$

3. Объем тела вращения будет равен:

V = Vц + 2Vк

V = 25π + 100π · 2 = 225π (см³)

Объем полученного тела равен 225π см³.