Question

За яких значень параметра а сума квадратів коренів рівняння x^2+ax+2a=0 дорівнює 5?

Answer 1

Ответ:

a = 5

Объяснение:

$x^{2} + ax + 2a = 0$

Найти при каком параметре $a$ сума корней квадратного уравнения равна 5, то есть $x_{1}^{2} + x_{2}^{2} = 5$.

По теореме Виета для действительных корней квадратного уравнения

$\left \{\begin{array}{l} D > 0 \\ x_{1} + x_{2} = -a \\ x_{1} x_{2} = 2a \end{array} \right$  $\left \{\begin{array}{l} a^{2} - 4 \cdot 1\cdot 2a > 0 \\ x_{1} + x_{2} = -a \\ x_{1} x_{2} = 2a \end{array} \right$

1)

$a^{2} - 4 \cdot 1\cdot 2a > 0$

$a^{2} - 8a > 0$

$a(a - 8) > 0$

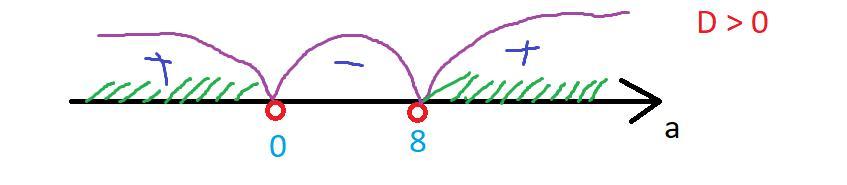
$a \in (-\infty;0) \cup (8;+\infty)$ система имеет решения при данных значениях параметра $a$.

2)

$x_{1}^{2} + x_{2}^{2} = (x_{1} + x_{2})^{2} - 2x_{1}x_{2} = (-a)^{2} - 2 \cdot 2a = a^{2} - 4a ;$

$x_{1}^{2} + x_{2}^{2} = 5$

$a^{2} - 4a = 5$

$a^{2} - 4a - 5 = 0$

$D =16 - 4 \cdot 1 \cdot (-5) = 16 + 20 =36 = 6^{2}$

$\boxed{a_{1} = \dfrac{4 + 6}{2} = \dfrac{10}{2} = 5}$

$a_{1} = \dfrac{4 - 6}{2} = \dfrac{-2}{2} = -1$ - не подходит так как $-1 \notin ((-\infty;0) \cup (8;+\infty))$.