Question

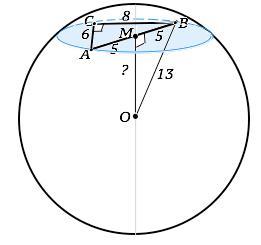
На поверхности шара есть три точки. Расстояние между ними 6 см, 8 см и 10 см. Радиус шара 13 см. Найдите расстояние от центра до плоскости, проходящей через эти точки​

Answer 1

Ответ:

12 см

Объяснение:

Дано:

Сфера (O; R); R = 13

$A, B, C \in (O;R) \\ AB = 6, BC = 8, AC = 10 \\ \: O' \in (ABC); \: \: OO' \perp (ABC)$

Найти: ОО' - ?

Решение:

Заметим, что

$AB^{2} + BC^{2} = {6}^{2} + {8}^{2} = 36 + 64 = 100 \\ \small AC^{2} = 10^{2} = 100 \: \: \: = > AB^{2} + BC^{2} = AC^{2}$

=> ∆АВС - прямоугольный, с гипотенузой АС.

А следовательно, АС - это диаметр окружности, описанной вокруг ∆АВС; середина АС - центр такой окружности

Так как любая точка пространства, равноудалённая от точек А, В, С, не лежащих на одной прямой, принадлежит прямой, перпендикулярной плоскости (АВС); и прямая проходит через центр окружности, описанной около треугольника с вершинами в данных точках.

Соответственно, если ОО' _|_ (АВС) =>

=> О' - центр окружности, описанной вокруг ∆АВС =>

$=> O' \in AC; \: O'A = O'C = \dfrac{10}{2} = 5$

Рассм. ∆АО'О:

ОО'_|_ (АВС) => ОО' _|_ АО' => уг.АО'О = 90°

=> ∆АО'О - прямоугольный, с гипотенузой АО = 13 см

По Т. Пифагора

$AO^2 = AO'^2+OO'^2 \\ OO'^2= AO^2- AO'^2\\ \: OO'= \sqrt{AO^2- AO'^2}$

$AO = 13; AO' = 5 => \\ = > \: OO' = \sqrt{13^2-5^2} = \sqrt{169 - 25} = \\ = \sqrt{144} = 12$

Ответ:

$OO' =12 \: cm$

Answer 2

Ответ: 12 см

Объяснение:

    Обозначим данные три точки  А, В и С. Они лежат на поверхности шара, следовательно, не лежат на одной прямой, и их можно объединить в треугольник АВС.

        Отношение сторон треугольника АВС со сторонами 6:8:10=3:4:5 – это отношение сторон «египетского» треугольника => данный треугольник – прямоугольный, в котором наибольшая сторона гипотенуза АВ=10 см.

     Расстояние от центра шара до вершин треугольника равно радиусу шара. => ∆ АВС  вписан в окружность, по которой проходит сечение шара плоскостью.

    По свойству окружности, описанной около прямоугольного треугольника, АВ является диаметром окружности в плоскости сечения шара.

     Центр шара и центр окружности, в которую вписан ∆ АВС, лежат на одной прямой, при этом центр М окружности - середина гипотенузы ∆ АВС.  

     Расстоянием от точки О ( центра шара) до плоскости ∆ АВС является длина отрезка, проведенного от точки перпендикулярно плоскости.  

     Рассмотрим схематический рисунок, сделанный согласно условиям задачи.

АВ - хорда, М - середина хорды.  => ОМ⊥АВ (свойство радиуса) АМ=ВМ=5 см

∆ ОМВ - прямоугольный.  Искомое расстояние ОМ=√(ОВ^2-ВМ^2)=√144=12 (см)