Question

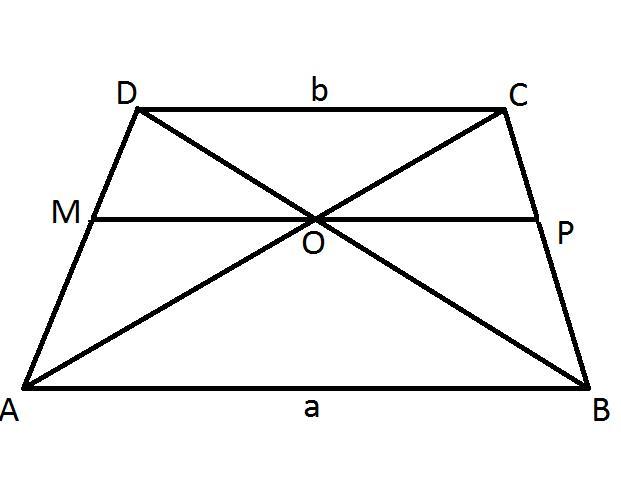
Большее основание трапеции равно 12 см. Прямая проходит через точку пересечения диагоналей трапеции параллельно её основаниям. Длина отрезка прямой, заключённого между боковыми сторонами трапеции, равна 8 см. Найти длину меньшего основания.​

Answer 1

Ответ:

b = 6

Пошаговое объяснение:

1) Треугольник AOB ~ DOC (∠AOB = ∠DOC, как вертикальный, ∠OAB = ∠COD, как накрест лежащий при параллельных DC и AB и секущей AC);

AB/DC = AO/OC = a/b, занчит,

AO/AC = AO/(AO+OC) = a/(a+b);

2) Треугольник ADC ~ AMO (∠DAC общий, ∠AMO = ∠ADC, как соответсвенный при параллельных MO и DC и секущей AD);

MO/DC = AO/AC = a/(a+b), отсюда MO = AO*DC/AC = ab/(a+b);

3) из 1) имеем, что AB/DC = BO/DO = a/b;

Треугольник DBC ~ OPB (∠DBC общий, ∠DCB = ∠OPB, как соответсвенный при параллельных OP и DC и секущей CB);

OP/DC = BO/DB = BO/(DO+OB) = a/(a+b), отсюда OP = BO*DC/DB = ab/(a+b);

4) MO = OP; MP = MO + OP = 2ab/(a+b).

5)Подставляем значения а = 12, MP = 8:

8 = 2*12b/(12 + b)

96 + 8b = 24b

b = 96/16 = 6