Question

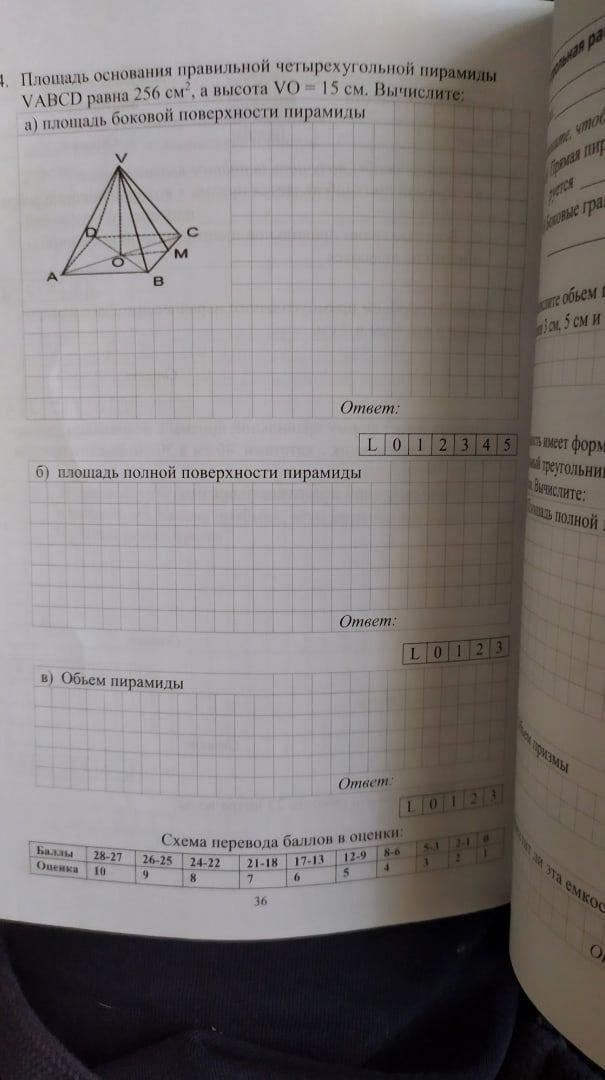
помогите решить весь номер 4

Answer 1

Ответ:

4)

а)

1) Найдём сторону основания пирамиды:

256 см² = √256 = 16 см

2) Теперь найдём площадь боковой поверхности правильной четырёхугольной пирамиды по стороне основания и высоте:

$s = \frac{4 \times a}{2} \sqrt{h {}^{2} + ( \frac{a}{2 \times \tan(45) } ) {}^{2} }$

Подставляем значения:

$s = \frac{4 \times 16}{2} \sqrt{15 {}^{2} + ( \frac{16}{2 \times \tan(45) } ) {}^{2} } = 32 \times \sqrt{225 +8 {}^{2} } = 32 \times \sqrt{225 + 64} = 32 \times \sqrt{289} = 32 \times 17 = 544 \: cm {}^{2}$

Ответ: S = 544 см²

б)

1) Найдём площадь полной поверхности правильной четырёхугольной пирамиды по стороне основания и высоте по этой формуле:

$s = \frac{4 \times a}{2} ( \frac{a}{2 \times \tan(45) } + \sqrt{h {}^{2} + ( \frac{a}{2 \times \tan(45) } ) {}^{2} } )$

Подставляем значения:

$s = \frac{4 \times 16}{2} ( \frac{16}{2 \times \tan(45) } + \sqrt{15 {}^{2} + ( \frac{16}{2 \times \tan(45) }) {}^{2} } ) = 32 \times (8 + \sqrt{225 + 8 {}^{2} } ) = 32 \times (8 + \sqrt{225 + 64} = 32 \times (8 + \sqrt{289} ) = 32 \times (8 + 17) = 32 \times 25 = 800 \: cm {}^{2}$

Ответ: S = 800 см²

в)

1) Найдём объём правильной четырёхугольной пирамиды по этой формуле:

$v = \frac{1}{3} ha {}^{2}$

Подставляем значения:

$v = \frac{1}{3} \times 15 \times 16 {}^{2} = 5 \times 256 = 1280 \: cm {}^{3}$

Ответ: V = 1280 см³

С площадями формулы большие, хахах