Question

70 БАЛЛОВ:
На гипотенузе AB прямоугольного треугольника АВС отмечена точка K, а на отрезке CK – точка N так, что AK : KB = KN : CN = 1 : 2. Найдите площадь треугольника ВСN, если AC = 9, BC = 16.

Answer 1

Ответ:

32 кв. ед.

Объяснение:

Найдем площадь прямоугольного треугольника АВС как половину произведения катетов:

$S_{ABC}=\dfrac{1}{2}AC\cdot BC=\dfrac{1}{2}\cdot 9\cdot 16=9\cdot 8=72$

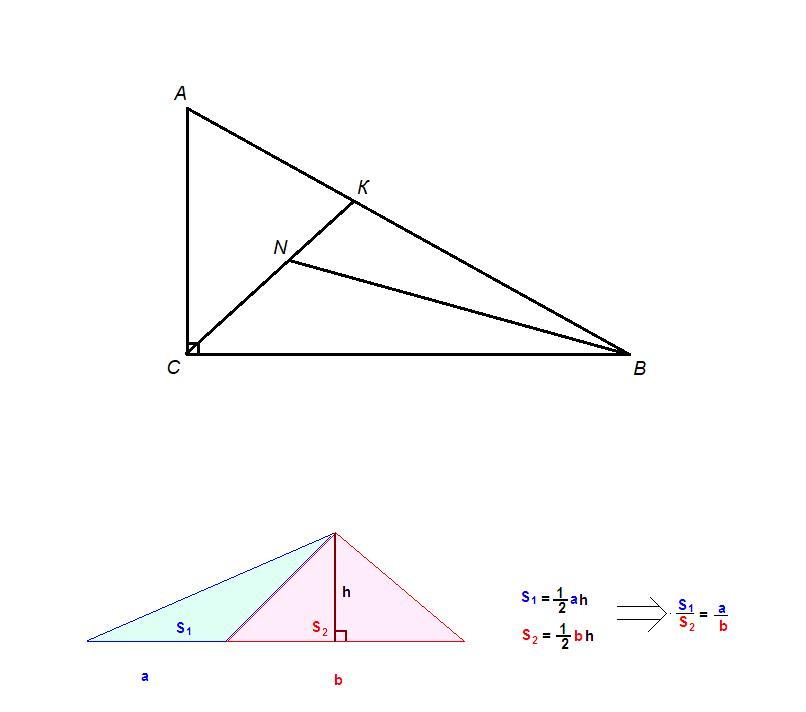
• Отношение площадей треугольников с общей высотой равно отношению сторон треугольников, к которым проведена эта высота (см. нижний рисунок).

В треугольниках АВС и ВСК можно провести общую высоту из вершины С, тогда

$\dfrac{S_{BCK}}{S_{ABC}}=\dfrac{KB}{AB}$

AK : KB = 1 : 2, значит KВ : AВ = 2 : 3

$S_{BCK}=S_{ABC}\cdot \dfrac{2}{3}=72\cdot \dfrac{2}{3}=24\cdot 2 = 48$

В треугольниках ВСК и BNC можно провести общую высоту из вершины B, тогда

$\dfrac{S_{BNC}}{S_{BCK}}=\dfrac{CN}{CK}$

KN : CN = 1 : 2, значит CN : CK = 2 : 3

$S_{BNC}=S_{BCK}\cdot \dfrac{2}{3}=48\cdot \dfrac{2}{3}=16\cdot 2 = 32$