Предмет: Алгебра,
автор: calendulas
Пожалуйста, помогите с заданием по алгебре (тригонометрия)
Задание на фотографии
Приложения:
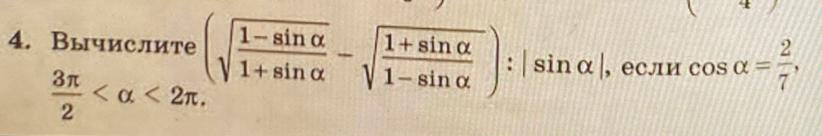
Ответы
Автор ответа:
1
Ответ:
в градусных мерах 270°<α<360°, то есть четвертая четверть.
В четвертой четверти синус отрицательный, поэтому напишем |sinα|=-sinα
Даём общий знаменатель в первой скобке
Если что
У нас
Ответ 7
Похожие вопросы
Предмет: Другие предметы,
автор: booch61
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: марина1318
Предмет: Алгебра,
автор: lassi3005