Предмет: Алгебра,
автор: andrejtkacuk023
25 баллов Решите систему уравнений
Приложения:
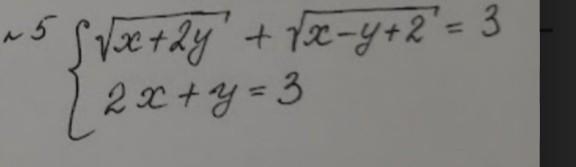
Ответы
Автор ответа:
0
Відповідь:
Відповідь:
andrejtkacuk023:
расшифруй первую часть
Похожие вопросы
Предмет: Английский язык,
автор: titan24
Предмет: Русский язык,
автор: алекса104
Предмет: Английский язык,
автор: BumblebeeDA
Предмет: Математика,
автор: Ggwphj
Предмет: Русский язык,
автор: egorkholod