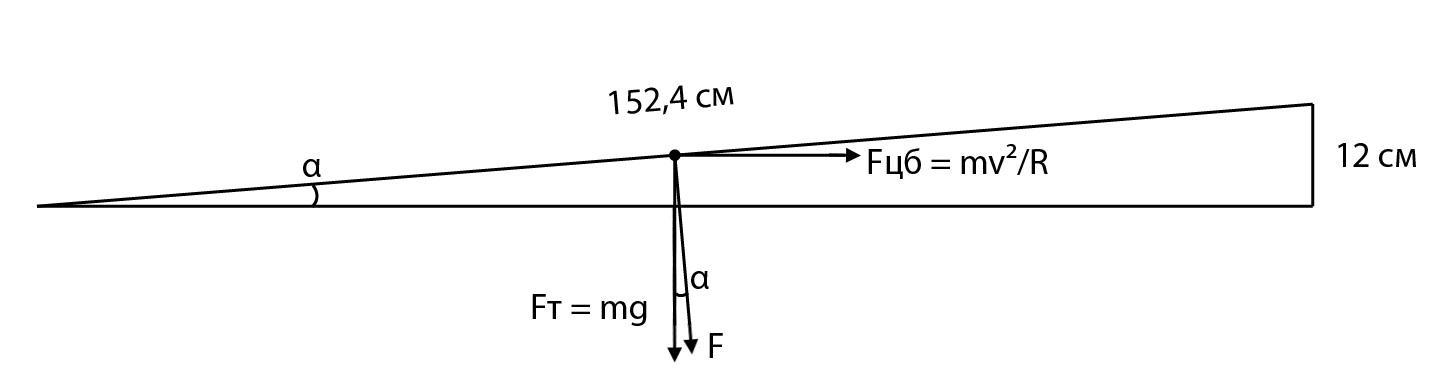
Поезд движется по закруглению радиусом 500 м. Ширина железнодорожной колеи 152.4 см. Наружный рельс расположен на 12 см выше внутреннего. При какой скорости движения поезда на закруглении колеса не оказывают бокового давления на рельсы? Построить поясняющий рисунок и указать все необходимые детали (векторы, углы).
Ответы
Ответ:
19,6 м/с
Объяснение:
На рельсы со стороны поезда во время поворота действует две силы.
1. Сила тяжести, направленная вертикально вниз:
Fт = mg
2. Внутренняя сила F, которая уравновешивает внешнюю центробежную силу, направленная горизонтально от центра закругления:
Fцб = mv²/R, где:
v - скорость поезда,
R - радиус дуги, по которой проходит путь.
Чтобы колеса поезда не оказывали бокового давления на рельсы, необходимо чтобы результирующая сила шла в направлении, отклонённом от вертикали на угол α (см рисунок).
Угол этот равен углу наклона пути и его можно рассчитать:
sin(α) = 12/152,4 ≈ 0,078
α ≈ 4,5°
Указанные силы так соотносятся с результирующей
Fт = F*cos(α)
Fцб = F*sin(α)
Отсюда:
F = Fт/cos(α) = Fцб/sin(α)
Fт*sin(α) = Fцб*cos(α)
mg*sin(α) = (mv²/R)*cos(α)
сокращаем на m, подставляем sin(α) = 0,078, cos(α) = 0,997, g = 9.8, R = 500 м
0,078*9.8 = 0,997*v²/500
0,7644*500/0,997 = v²
v ≈ √383 ≈ 19,6 м/с ≈ 70 км/ч