Две окружности касаются внешним образом в точке А. одна прямая касается их в точках В и С.найдите угол ВАС
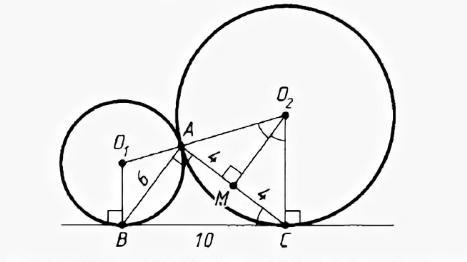
(рисунок примерно такой, только без значений отрезков)
Ответы
Ответ:
Проводя касательные к окружности, не забывайте отмечать ПРЯМЫЕ (!) углы,
которые касательная образует с радиусами, проведёнными в точки касания.
Две окружности касаются внешним образом в точке А (вар. 97)
ТА и ТС - касательные, проведённые из одной точки Т к маленькой окружности.
ТА и ТВ - касательные, проведённые из одной точки Т к большой окружности.
По свойству касательных ТА = ТС и ТА = ТВ. Получаем, что ТС = ТВ = ТА.
Таким образом, АТ - медиана треугольника АВС, которая равна половине ВС -
стороны, к которой она проведена. Значит, треугольник АВС - прямоугольный.
(т. Т равноудалена от вершин треугольника, т.е. является центром описанной
около АВС окружности. ВС - её диаметр, на диаметр опирается прямой угол).
Чтобы найти площадь треугольника АВС, проведём стандартные вычисления.
В прямоугольной трапеции опустим высоту из вершины тупого угла. Найдём её.
18(C4). Две окружности касаются внешним образом в точке А (вар. 97)
В треугольнике АВС знаем сторону ВС. Для полного счастья не хватает высоты АН.
18(C4). Две окружности касаются внешним образом в точке А (вар. 97)
Разобьём её на два отрезка АК и КН и найдём каждый из цветных треугольников.
18(C4). Две окружности касаются внешним образом в точке А (вар. 97)
Воспользуемся при этом попарным подобием треугольников и данными задачи:
Осталось найти площадь, зная гипотенузу треугольника и высоту, проведённую к ней:
Ответ: 12,8
Объяснение: