Question

8. (2 б) У прямокутному трикутнику KLN (кут L – прямий) на гіпотенузі взяли

точку S так, що ∠SKL = ∠KLS. Доведіть, що SL =SN . Даю 40 балов

Answer 1

Ответ:

SL = SN

Объяснение:

Обозначим равные углы:

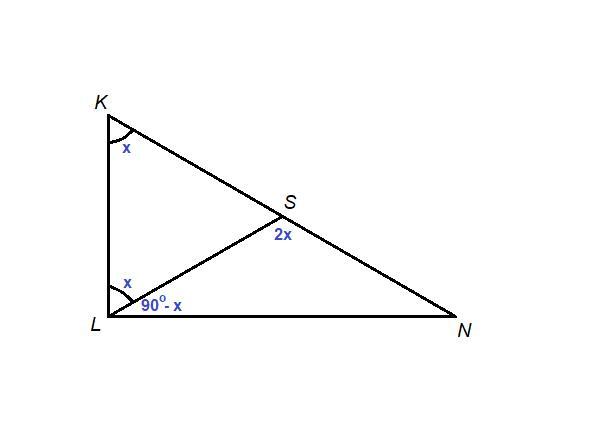
∠SKL = ∠KLS = x

Тогда ∠LSN = 2х как внешний угол треугольника SKL.

∠SLN = ∠KLN - ∠KLS = 90° - x.

Выразим угол SNL (сумма углов треугольника равна 180°):

∠SNL = 180° - (∠SLN + ∠LSN)

∠SNL = 180° - (90° - x + 2x) = 180° - 90° - x = 90° - x

Получили, что ∠SNL = ∠SLN = 90° - x, значит

ΔSLN равнобедренный с основанием LN, то есть

SL = SN.