Question

СРОЧНО!!! ПОМОГИТЕ!!!
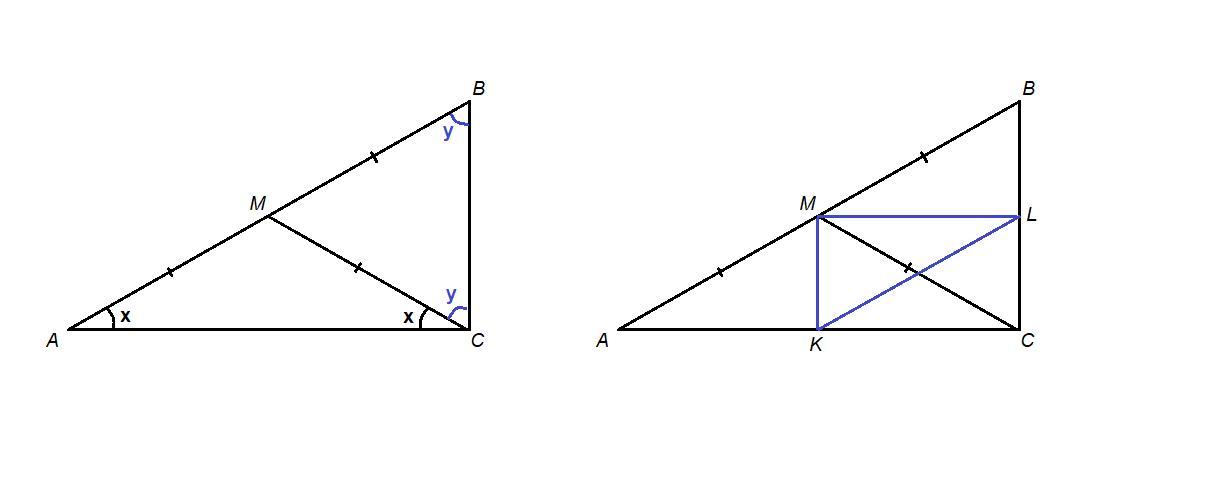
В треугольнике АВС медиана СМ= 1/2 АВ, в треугольниках АМС И ВМС проведены биссектрисы МК и МL соответственно. Найдите периметр треугольника АВС, если периметр треугольника КМL=17см.

Answer 1

Ответ:

$P_{ABC}=34$ см

Объяснение:

Докажем утверждение:

• если медиана равна половине стороны, к которой она проведена, то треугольник прямоугольный, и медиана проведена к гипотенузе.

М - середина АВ, СМ = 1/2 АВ, то есть

АМ = ВМ = СМ.

ΔАСМ равнобедренный, значит ∠МАС = ∠МСА = х.

ΔВСМ равнобедренный, значит ∠МВС = ∠МСВ = y.

Сумма углов треугольника равна 180°.

∠А + ∠В + ∠АСВ = 180°

x + y + (x + y) = 180°

2(x + y) = 180°

x + y = 90°

∠АСВ = 90°

____________________

ΔАМС - равнобедренный, значит

МК - биссектриса и высота.

МК║ВС как перпендикуляры к одной прямой, а так как М - середина АВ, то К - середина АС по теореме Фалеса.

ΔВМС - равнобедренный, значит

МL - биссектриса и высота.

МL║AС как перпендикуляры к одной прямой, а так как М - середина АВ, то L - середина BС по теореме Фалеса.

Итак, МК, ML, KL - средние линии треугольника АВС.

• Средняя линия треугольника параллельна третьей стороне и равна ее половине.

$P_{ABC}=AB+BC+AC$

$\boldsymbol{P_{ABC}}=2KL+2MK+2ML=2(KL+MK+ML)=$

$=2\cdot P_{KML}=2\cdot 17\boldsymbol{=34}$ см