Предмет: Алгебра,
автор: eleonaise
[3] Решить задание...
Приложения:
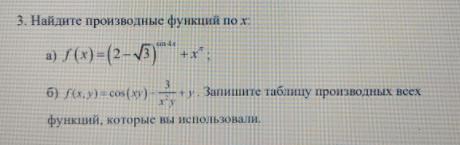
Ответы
Автор ответа:
2
Ответ: во вложении
Объяснение:
во вложении
Приложения:

eleonaise:
благодарю ♥
Автор ответа:
1
Ответ:
Пользуемся правилами дифференцирования сложной функции .
При нахождении производной по переменной х считаем переменную у постоянной ( производная константы = 0 ) .
Похожие вопросы
Предмет: Английский язык,
автор: poldina80
Предмет: Окружающий мир,
автор: нік35
Предмет: Русский язык,
автор: gubichlida
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: AzilotikGame