[1] Решить задание...
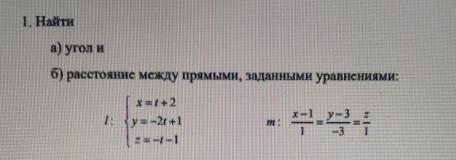
Ответы
направляющий вектор первой прямой {1;-2;-1}
вторую прямую перепишем
(х-1)/1= t ⇒х= t+1
(у-3)/(-3)= t ⇒у=-3 t+3
z/1= t⇒z= t
направляющий вектор {1;-3;1}
найдем скалярное произведение и модули векторов, а затем косинус угла между ними.
1*1-2*(-3)-1*1=6
√(1²+(-2)²+1²)=√6
√(1²+(-3)²+1²)=√11
cosφ=6/(√6*√11)=√(6/11)≈073854895; φ≈42°
расстояние между прямыми:
возьмем по точке на прямых, например, при t=0, на первой прямой
М₁(2;1;-1), а на второй М₂(1;3;0) координаты вектора →М₁М₂(-1;2;1)
найдем смешанное произведение векторов →М₁М₂; {1;-2;-1}; {1;-3;1}
-121
1-2-1
1-31
видим. что первые две строки определителя пропорциональны, т.е. смешанное произведение равно нулю. векторы компланарны. и расстояние между прямыми равно нулю.
Ответ 42°; 0
Ответ:
Прямые не параллельны, так как координаты их направляющих векторов не пропорциональны .
Ищем расстояние между скрещивающимися прямыми как частное от деления модуля смешанного произведения направляющих векторов и вектора М₁М₂ на модуль векторного произведения направляющих векторов:
Получили, что смешанное произведение трёх векторов равно 0, значит прямые компланарны . Вычислять модуль векторного произведения, записанного в знаменателе, не имеет смысла. Расстояние между прямыми равно 0.
Косинус угла между прямыми находится по формуле .
Угол можно найти приближённо .