Предмет: Алгебра,
автор: Cef1rka
Решить систему уравнений
Приложения:
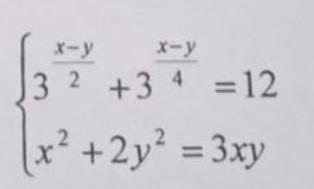
Ответы
Автор ответа:
1
Ответ:
(8; 4)
Объяснение:
Рассмотрим нижнее уравнение:
Замена переменной:
По Т. Виета:
Обратная замена:
Подстановка в начальную систему
Решим (1.1)
Решим (1.2)
По Т. Виетта:
Решим (2.1)
Решим (2.2)
Нашли х = 8
Из системы находим значение у
Получили ответ: точку (8; 4)
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: Kirillfaorov
Предмет: Русский язык,
автор: дети23
Предмет: Английский язык,
автор: kirushina2000
Предмет: Математика,
автор: daniil34567834
Предмет: Химия,
автор: Hellii