Question

Знайти об’єм тіла обертання. Фігура, обмежена прямими y=2x, x=5 і y=0, обертається навколо осі ОХ.

Answer 1

Ответ:

$\boxed{\boxed{V = \dfrac{500 \pi }{3}}}$ кубічних одиниць

Пошаговое объяснение:

За теоремою об'єм тіла обертання можна знайти формулою:

$\boxed{\displaystyle V = \pi \int\limits^a_b {f^{2}(x)} \, dx}$, при умові, що функія $f(x)$ неперервна на відрізку $[a;b]$ і обмежена прямими x = a, x = b і $y =0$.

За умовою фігура обмежена прямими:

$f(x) = 2x$

$b =x = 5$

$y = 0$

Знайдемо точку перетину $y$ і $f(x)$

$2x = 0 \Longrightarrow x = 0$

Функція $f(x)$ неперервна на відрізку від [0;5], так як є лінійною функцією, а за властивістю лінійної функції вона є неперервною.

Отже, фігура обмежена прямими:

$f(x) = 2x$

$a = 0$

$b = 5$

$y = 0$

Об'єм тіла обертання:

$\displaystyle V = \pi \int\limits^5_0 {(2x)^{2}} \, dx = \pi \int\limits^5_0 {4x^{2} } \, dx = 4\pi \int\limits^5_0 {x^{2} } \, dx = 4\pi \cdot \frac{x^{3}}{3} \bigg |_0^5 = \frac{4\pi }{3} \bigg (5^{3} - 0^{3} \bigg) =$

$= \dfrac{4\pi \cdot 125}{3} = \dfrac{500 \pi }{3}$ кубічних одиниць.

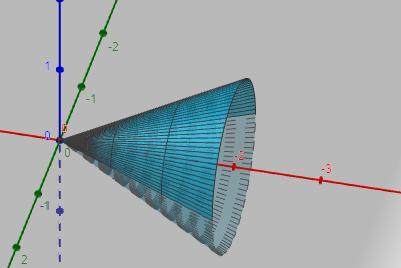
Зазначимо, також, що при обертанні утворюється тіло, яке має назву прямий конус.