Предмет: Математика,
автор: zerogrifefcervdv
Необходимо решить задание. Желательно быстрее
Приложения:
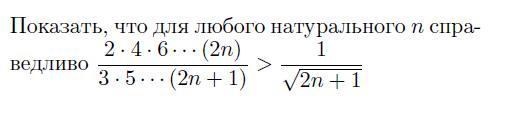
Ответы
Автор ответа:
0
Пошаговое объяснение:
Решим по индукции.
База:
2/3 > 1/, т.к.
Если верно равенство для n и верно
Возведя в квадрат, получим
Возможно тогда и только тогда, когда
или
что равносильно
Похожие вопросы
Предмет: Окружающий мир,
автор: 5473894
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: мага32
Предмет: Математика,
автор: noshnovosel
Предмет: Русский язык,
автор: varvaraperedvetova