Розв'яжіть рівняння
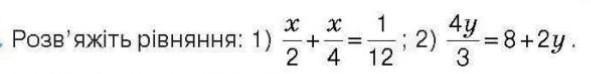
Ответы
Ответ:
1. х = 1/9
2. у = -12
Пошаговое объяснение:
1. х/2 + х/4 = 1/12
2х/4 + х/4 = 1/12
3х/4 = 1/12
3х = 1/12 * 4 3х = 1/3 х = 1/3 : 3 х = 1/3 * 1/3 х = 1/9
2. 4у/3 = 8 + 2у
4у/3 - 2у = 8
4у/3 - 6у/3 = 8
-2у/3 = 8 -2у = 8 * 3 -2у = 24 у = 24/(-2) у = -12
Ответ:
Пошаговое объяснение:
Задание 1.
Найдем НОК 2 и 4. Определение: Наименьшим общим кратным (НОК) 2 и 4 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (2 и 4). Поскольку 4 делится нацело на 2, НОК этих чисел равно самому числу 4. ⇒ 4 - общий знаменатель для дробей, которые находятся в левой части уравнения. Дописываем дополнительные множители числителям:
Сложим дроби в левой части уравнения. Знаменатели одинаковые, складываем числители.
Это пропорция. Основное свойство пропорции: Произведение крайних членов равно произведению средних. Перемножим крест на крест ⇒
Правило: Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель ⇒
Задание 2.
Здесь я поступлю иначе. Умножим обе части уравнения на 3, чтобы избавиться от дробного выражения ⇒
В левой части остается одночлен "4у". В правой используем распределительный закон умножения: a(b+c)=ab+ac.
Переносим неизвестные элементы в одну сторону, известные в другую, при этом знаки элементов меняем на противоположные ⇒
Группируем и приводим подобные члены в левой части уравнения.