Question

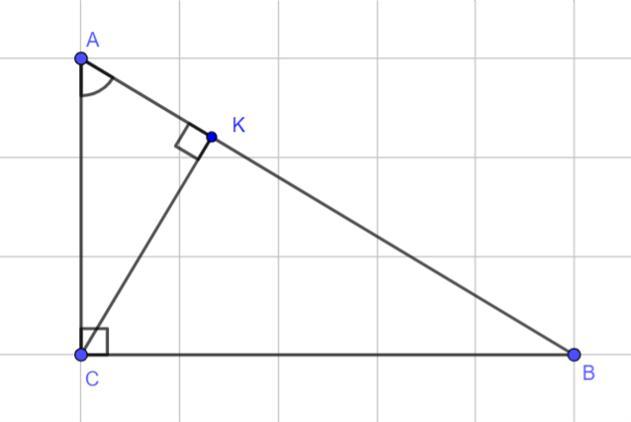
Знайдіть висоту прямокутного трикутника АВС проведену до гіпотенузи якщо гіпотенуза АВ=с а кут А=а

Дано і ТД​

Answer 1

Дано:

∠C = 90°,

AB = c

∠A = α

CK ⊥ AB

Знайти:

CK

                                        Розв'язання:

Нам треба виразити висоту трикутника, проведену до гіпотенузи, через його гіпотенузу та гострий кут.

За метричними співвідношеннями в прямокутному трикутнику:

$\displaystyle CK = \frac{BC\cdot AC}{AB}$

За означенням синуса гострого кута прямокутного трикутника:

$\displaystyle sin \angle A = \frac{BC}{AB}$

Звідси, BC = AB · sin ∠A

За означенням косинуса:

$\displaystyle cos \angle A = \frac{AC}{AB}$

Звідси, AC = AB · cos ∠A

Підставимо у формулу вище:

$\displaystyle CK = \frac{AB \cdot sin \angle A \cdot AB \cdot cos \angle A}{AB} = AB \cdot sin \angle A \cdot cos \angle A = c\ sin\alpha \ cos\alpha.$

Відповідь:

$c\ sin\alpha \ cos\alpha.$