Question

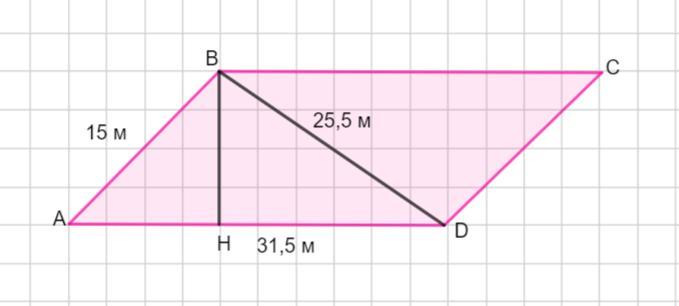
Стороны параллелограмма равны 15м 31,5м одна из диагоналей 25,м найди меньшую высоту параллелограмма

Answer 1

Ответ:

Меньшая высота параллелограмма 12 см.

Пошаговое объяснение:

Пусть дан параллелограмм АВСD.

АВ = 15 м,  АD = 31,5 м, диагональ АС =25,5 м.

Меньшая высота параллелограмма проведена к большей стороне АD.

ВН - высота, проведенная к стороне АD.

Данная высота является и высотой Δ АВD.

Найдем высоту треугольника через площадь.

Площадь треугольника найдем по формуле Герона:

$S= \sqrt{p(p-a)(p-b)(p-c) } ,$ где

$p= \dfrac{a+b+c}{2} , a,b,c -$  стороны треугольника.

$p= \dfrac{15+31,5+25,5}{2} =\dfrac{72}{2} =36$

$S= \sqrt{36\cdot(36-15)\cdot(36-31,5)(36-25,5)} =\sqrt{36\cdot 21\cdot 10,5\cdot 4,5} =\\\\=\sqrt{9\cdot 21\cdot2\cdot10,5\cdot2\cdot4,5} =\sqrt{9\cdot21\cdot21\cdot9} =9\cdot21= 189$

Площадь данного треугольника равна 189 м ².

Найдем площадь этого же треугольника как полупроизведение стороны на высоту, проведенную к этой стороне.

$S= \dfrac{1}{2} \cdot AD\cdot BH;\\\\BH= \dfrac{2S}{AD} ;\\\\BH= \dfrac{2\cdot189}{31,5} =\dfrac{2\cdot189\cdot2}{31,5\cdot2} =\dfrac{4\cdot189 }{63} =\dfrac{4\cdot63\cdot 3}{63} =4\cdot3=12$

Значит, высота треугольника, а это и высота параллелограмма равна 12 м.