Question

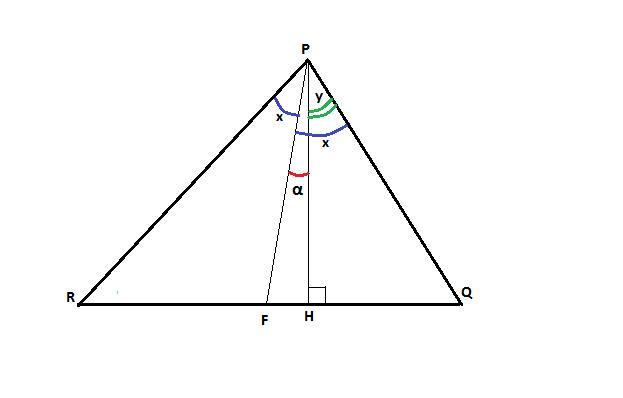
Отрезки `PH` и `PF` являются высотой и биссектрисой треугольника `PQR` соответственно. Известно, что ∠PQR-∠PRQ=22°. Найдите ∠HPF

Answer 1

Ответ:

∠HPF = α = 11°

Объяснение:

Дан треугольник PQR, у которого ∠PQR - ∠PRQ = 22°.

Даны высота треугольника PH и биссектриса PF.

Найти ∠HPF.

Решение:

Смотрите рисунок.

Так как PF - биссектриса ∠RPQ, то:

∠RPF = ∠FPQ = x

∠PHQ = ∠PHR = 90°

∠HPQ = y = 90° - ∠PQR

∠PQR = 90° - y

∠HPF = α = x - y

x = y + α

x + y = 90° - ∠PRQ

∠PRQ = 90° - (x + y) = 90° - (y + α + y) = 90° - 2y - α

По условию:

∠PQR - ∠PRQ = 22°

90° - y - (90° - 2y - α) = 22°

90° - y - 90° + 2y + α = 22°

y + α = 22°

Но y + α = x = 22°

∠RPQ = 2x = 2*22° = 44°

По теореме об углах треугольника:

∠RPQ + ∠PRQ + ∠PQR = 180°

Получаем систему:

{ ∠PQR + ∠PRQ = 180° - ∠RPQ = 180° - 44° = 136°

{ ∠PQR - ∠PRQ = 22°

Решая эту систему, получаем:

2*∠PQR = 136° + 22° = 158°

∠PQR = 158° : 2 = 79°

∠PRQ = 136° - ∠PQR = 136° - 79° = 57°

Из треугольника PHR:

∠RPH  = x + α = 90° - ∠PRQ = 90° - 57° = 33°

∠HPF = α = ∠RPH - x = 33° - 22° = 11°