Question

Окружность вписанная в прямоугольный треугольник точкой касания делит гипотенузу на отрезки разность которых 7 см а сумма 13 см найди радиус вписанной окружности.

Answer 1

Ответ:

2 см

Объяснение:

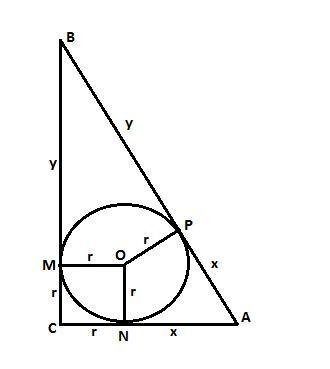
Смотрите рисунок.

Обозначим x и y части, на которые точка P делит гипотенузу.

Радиусы OM и ON отрезают на катетах такие же отрезки x и y.

По условию:

{ y - x = 7

{ y + x = 13

Складываем уравнения:

2y = 20

Отсюда y = 10 см, x = 3 см.

Из теоремы Пифагора:

BC^2 + AC^2 = AB^2

(r + y)^2 + (r + x)^2 = (x + y)^2

(r + 10)^2 + (r + 3)^2 = 13^2

r^2 + 20r + 100 + r^2 + 6r + 9 = 169

2r^2 + 26r = 60

Делим всё на 2:

r^2 + 13r - 30 = 0

D = 13^2 - 4*1(-30) = 169 + 120 = 289 = 17^2

r1 = (-13 - 17)/2 = -30/2 = -15 < 0 - не подходит.

r2 = (-13 + 17)/2 = 4/2 = 2 см - подходит.