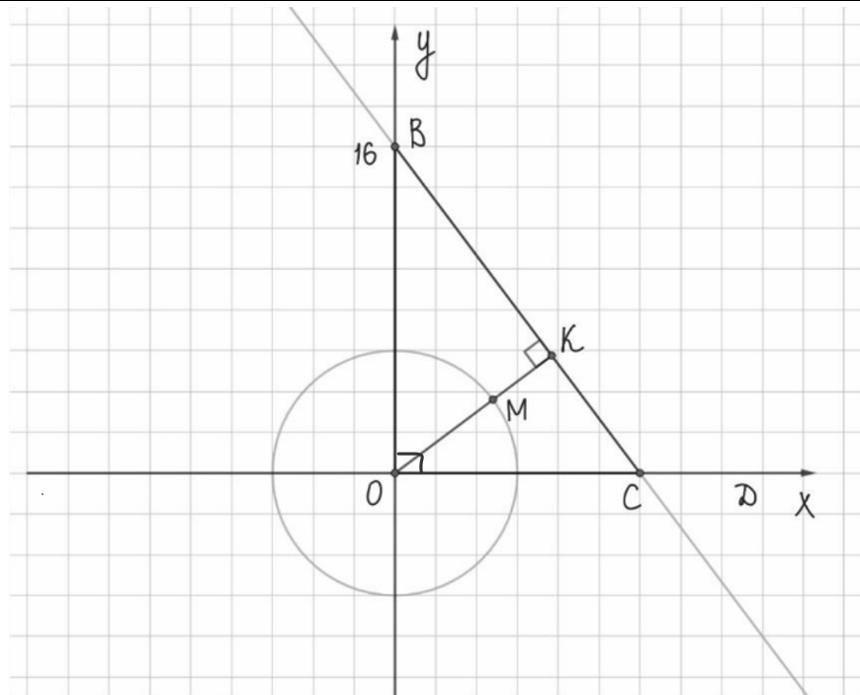
Найти кратчайшее расстояние от окружности до прямой! ПОМОГИТЕ ПОЖАЛУЙСТА, ДАЮ 100 БАЛЛОВ
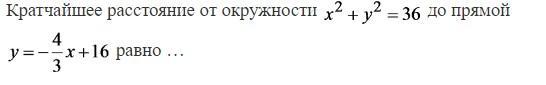
Ответы
Ответ: кратчайшее расстояние от данной окружности до прямой равно 3,6.
Объяснение:
Общий вид уравнения окружности:
, где а и b — координаты центра.
Нам дана окружность x² + y² = 36.
Судя по уравнению, ее центр имеет координаты (0; 0), а радиус равен √36 = 6.
Общий вид уравнения прямой:
, где k — угловой коэффициент, равный тангенсу угла между прямой и положительным направлением оси ОХ, а b — свободный член, равный ординате точки пересечения прямой с осью ОУ.
Нам дана прямая
Судя по уравнению, тангенс угла между ней и положительным направлением ОХ равен и прямая пересекает ОУ в точке (0; 16).
Расстояние от точки до прямой — это перпендикуляр, проведенный из этой точки на прямую.
Поэтому, если мы из центра окружности опустим перпендикуляр на прямую, то кратчайшим расстоянием от окружности до прямой будет отрезок, соединяющий конец радиуса и основание перпендикуляра (на рисунке это отрезок МК).
______________________________
Дано:
∠BOC = 90° (потому что координатные оси перпендикулярны);
BO = 16;
tg∠BCD = ;
ОК ⊥ ВС;
ОМ = 6.
Найти:
МК.
Решение:
∠BCD и ∠BCO — смежные, а значения тангенсов смежных углов противоположны.
Поэтому tg∠BCO = .
Поскольку тангенс угла равен отношению противолежащего ему катета к прилежащему, можем записать такую пропорцию:
Выразим ОС:
.
По теореме Пифагора:
BC² = BO² + OC² = 16² + 12² = 256 + 144 = 400
BC = √400 = 20.
ОК — высота прямоугольного треугольника, проведенная к гипотенузе.
По метрическим соотношениям:
.
Вычтем отсюда радиус окружности:
МК = ОК - ОМ = 9,6 - 6 = 3,6.