Предмет: Математика,
автор: folot1789
Найти производную y=f(x)
фото прикрепил
Приложения:
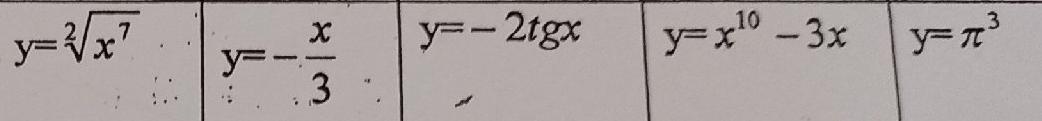
Simba2017:
1)y=x^(7/2)=x^3.5; y`=3.5x^2/5
2)y`=-1/3
3)y=-2/cos^2x
4)10x^9-3
5)0
Ответы
Автор ответа:
1
1)y'=(x⁷/²)'=(7x⁵/²)/2=3.5*x²√x, по формуле производной степенной функции у'=(xⁿ)'=n*xⁿ⁻¹
2)y'=-1/3-производная х равна 1, константа выносится за знак производной.
3)y'=-2/cos²x -табличный, константу вынесли за знак производной.
4) y'=10x⁹-3-производные степенной функции. см. выше.
5) y'=0 - производная константы равна нулю.
Автор ответа:
1
Ответ:
Пользуемся правилами дифференцирования функций и таблицей производных .
Похожие вопросы
Предмет: Українська мова,
автор: Іринка18042003
Предмет: Английский язык,
автор: sonyauralpelmeny
Предмет: Русский язык,
автор: jannasokolowa
Предмет: Алгебра,
автор: vodila22822
Предмет: География,
автор: mzeflina