Question

Помогите, пожалуйста, решить. Прямая, не параллельная стороне AC треугольника ABC, делит каждую из двух других сторон в отношении 3:4. при этом образуется треугольник BMK и четырехугольник AMKC. Площадь четырехугольника AMKC равна 111. Найти площадь треугольника ABC

Answer 1

Ответ:

147 кв. ед.

Объяснение:

Если бы прямая МК делила стороны ВС и АВ в отношении 3 : 4, считая от вершины В, то МК была бы параллельна АС (теорема, обратная теореме Фалеса).

Тогда ВМ : МА = 3 : 4, а ВК : КС = 4 : 3.

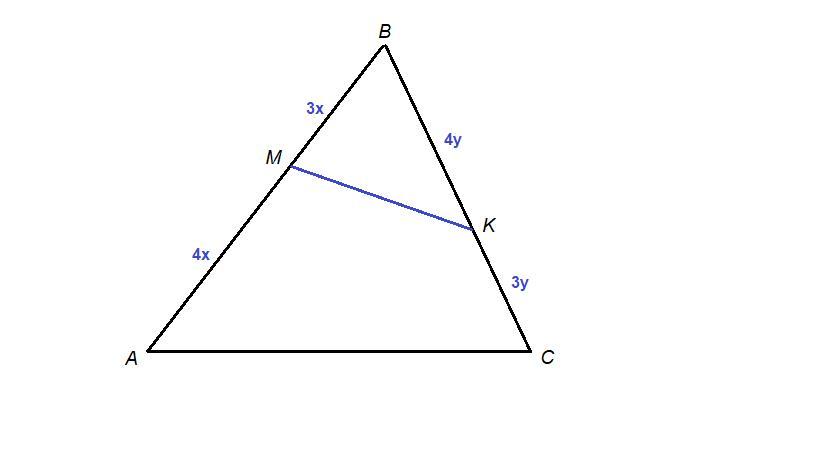
Введем обозначения как на рисунке.

Площадь треугольника АВС:

$S_{ABC}=\dfrac{1}{2}AB\cdot BC\cdot \sin\angle B$

$S_{ABC}=\dfrac{1}{2}\cdot 7x\cdot 7y\cdot \sin\angle B=\dfrac{49xy\; \sin\angle B}{2}$

Площадь треугольника ВМК:

$S_{BMK}=\dfrac{1}{2}BM\cdot BK\cdot \sin\angle B$

$S_{BMK}=\dfrac{1}{2}\cdot 3x\cdot 4y\cdot \sin\angle B=6xy\; \sin\angle B$

Найдем отношение площадей этих треугольников:

$\dfrac{S_{ABC}}{S_{BMK}}=\dfrac{49xy\; \sin\angle B}{2}\cdot \dfrac{1}{6xy\; \sin\angle B}=\dfrac{49}{12}$

То есть площадь треугольника ВМК составляет 12 частей, а площадь треугольника АВС - 49 частей.

Тогда площадь четырехугольника АМКС составляет:

49 - 12 = 37 частей.

Итак,

$\dfrac{S_{ABC}}{S_{AMKC}}=\dfrac{49}{37}$

$S_{ABC}=\dfrac{S_{AMKC}\cdot 49}{37}=\dfrac{111\cdot 49}{37}=3\cdot 49=147$