Найдите 5 первых элементов последовательности
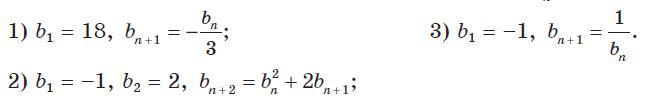
Ответы
Ответ:
1) 18; -6; 2; -2/3; 2/9.
2) b₁ = -1; b₂ = 2; b₃ = 5; b₄ = 14; b₅ = 53.
3) b₁ = b₂ = b₃ = b₄ = b₅ = -1.
Объяснение:
Найти 5 первых элементов последовательностей по заданным рекуррентным формулам.
1)
Здесь дана геометрическая прогрессия, так как каждый последующий член прогрессии равен предыдущему, умноженному на одно и то же число.
Первый член равен 18, а знаменатель прогрессии равен -1/3. Можно также вычислить 5 членов прогрессии по общей формуле члена геометрической прогрессии.
2) b₁ = -1; b₂ = 2; bₙ₊₂ = bₙ² + 2bₙ₊₁.
Вычислим 5 членов последовательности по заданным формулам.
Два члена уже известны.
b₁ = -1; b₂ = 2;
b₃ = b₁² + 2b₂ = (-1)² + 2·2 = 5;
b₄ = b₂² + 2b₃ = 2² + 2·5 = 14;
b₅ = b₃² + 2b₄ = 5² + 2·14 = 25+28 = 53.
3)
Все члены этой последовательности равны -1, так как любой ее член получается делением 1 на (-1).