Предмет: Алгебра,
автор: twiinklllelonelystar
Помогите пожалуйста !!! Плачу 40 баллов !!!!
Приложения:
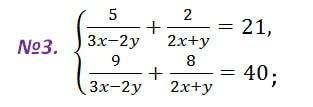
Ответы
Автор ответа:
1
Ответ:
Выполним замену , тогда система примет вид
Решаем систему методом сложения.
Похожие вопросы
Предмет: Русский язык,
автор: gunay0912
Предмет: Русский язык,
автор: dudu4
Предмет: Русский язык,
автор: Лера3425635
Предмет: Математика,
автор: Raana66
Предмет: Русский язык,
автор: erkebulnova