Предмет: Алгебра,
автор: 34577788az
ОЧЕНЬ НУЖНО!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
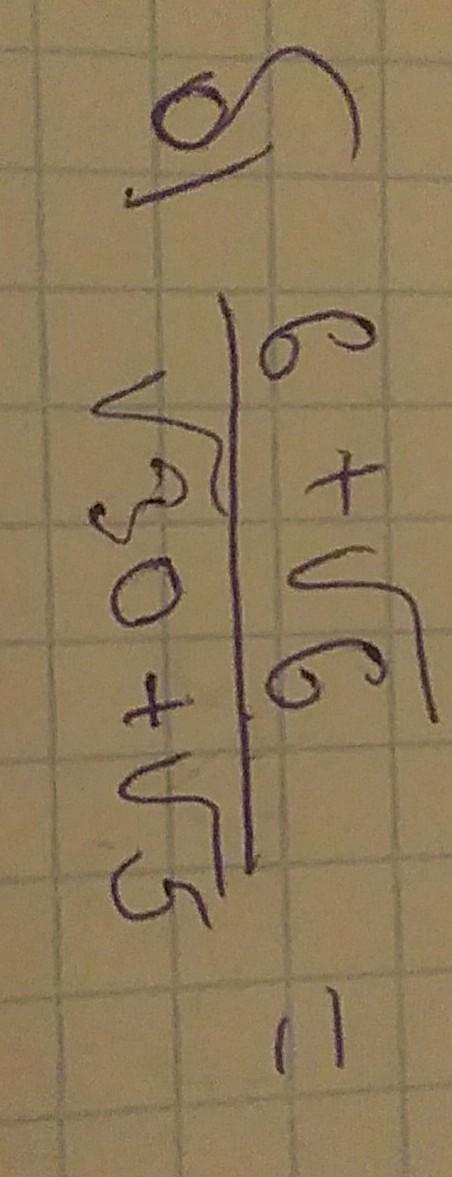
Ответы
Автор ответа:
0
Так как ничего не сказано про то,что именно нужно сделать , то рассматриваем два варианта
1) Сократить дробь
2) Упростить выражение,путем избавления от иррациональности знаменателе дроби
1) Ход действий :
Раскладываем выражение на множители,которые можно представить в виде сомножителей,и далее сократить то,что одинаковое
2) Ход действий :
Умножаем дробь на выражение сопряженное знаменателю, тоесть на значения с одинаковыми действительными частями и равными по абсолютной величине, но противоположными по знаку
Так же используя формулу сокращенного умножения разности квадратов - a^2-b^2=(a-b)(a+b) , упростим выражение
Сокращаем противоположные слагаемые, приводим подобные
Похожие вопросы
Предмет: Русский язык,
автор: Ñēбø
Предмет: Русский язык,
автор: мария1474
Предмет: Русский язык,
автор: Димас543u
Предмет: Литература,
автор: ksusha8456
Предмет: Математика,
автор: Barmolei