Question

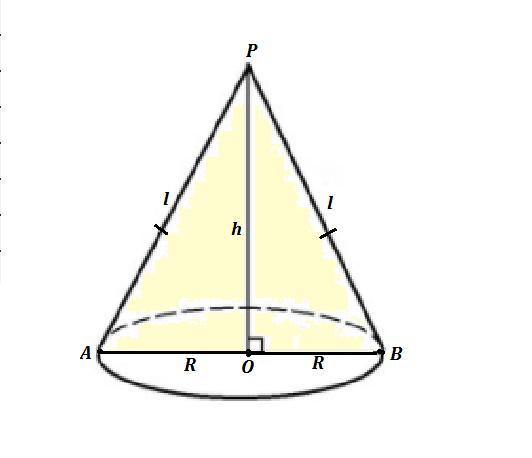
Площадь боковой поверхности конуса больше площади его основания в 3 раза. Найдите объем конуса, если площадь его осевого сечения равна 8 корень 2 см^2. . ​

Answer 1

осевое сечение конуса - это равнобедренный треугольник,  боковые сторонами которого - образующие конуса, а основанием-диаметр основания конуса. высота конуса равна высоте осевого сечения.

Объем конуса равен (1/3)πR²h

πRL- боковая поверхность конуса,

πR²-площадь основания.

площадь осевого сечения равна 2R*h/2=R*h

Площадь боковой поверхности конуса больше площади его основания в 3 раза.⇒ πRL=3*πR²⇒L=3R, высоту найдем из прямоуг. треугольника, составленного из высоты, радиуса и образующей.

√((3R)²-R²)=2√2R=h

по условию R*h=8√2; т.к. 2√2R=h⇒2√2R=8√2;R²=4, R=2,

h=2√2R=2√2*2=4√2

Объем конуса равен ( 1/3)πR²h=(1/3)π*4*4√2=(16√2)π/3/cм³/

Answer 2

Ответ:

Дан конус. Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось  конуса РО . Осевое сечение конуса — это равнобедренный  ΔАРВ , АР=ВР=$l$ ,  AB=2R - диаметр основания, h=РО - высота конуса и высота ΔАРВ , AO=BO=R .

Площадь боковой поверхности конуса  $S_{b}=\pi R\, l\ \ ,$ площадь основания конуса  $S_{o}=\pi R^2$  . По условию  $S_{b}=3S_{o}\ \ \Rightarrow \ \ \ \pi R\, l=3\pi R^2$  ,

$l=3R$

Найдём высоту осевого сечения из прямоугольного ΔАРO .

$PO^2=AP^2-AO^2\ \ \to \ \ \ h^2=l^2-R^2=(3R)^2-R^2=8R^2\ \ ,\\\\h=\sqrt{8R^2}=2\sqrt2R$

Площадь осевого сечения известна и может быть найдена таким образом  

 $S_{APB}=\dfrac{1}{2}\cdot AB\cdot PO=\dfrac{1}{2}\cdot 2R\cdot 2\sqrt2R=2\sqrt2R^2\ \ ,\ \ 2\sqrt2R^2=8\sqrt2\ \ ,\\\\R^2=4\ \ ,\ \ R=2\ (sm)$

Объём конуса  $V=\dfrac{1}{3}\cdot S_{o}\cdot h=\dfrac{1}{3}\cdot \pi R^2\cdot 2\sqrt2R=\dfrac{2\sqrt2}{3}\, \pi R^3=\dfrac{2\sqrt2}{3}\, \pi \cdot 2^3=\dfrac{16\sqrt2}{3}\, \pi \ \ (sm^3)$