Предмет: Алгебра,
автор: chelique
(1/8)^(x^2 + 1) > (1/32)^(2*x)
решить уравнение (неравенство)
Приложения:
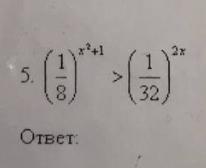
Ответы
Автор ответа:
0
Ответ:
Решением неравенства является интервал
Объяснение:
т.к.
и
то
т.к. функция
- убывает, то при переходе к показателям степеней знак неравенства меняем, т.е.
Найдем нули
D = 100-4*3*3=64
значит наше неравенство можно переписать так:
3*(х-)*(х-3) < 0
методом интервалов найдем решение (определим знак неравенства в каждом из промежутков)
__+___.___-___.___+____
Ответом для нашего неравенства (нам надо где <0) будет интервал
katjushika:
какую?
если только позже
Похожие вопросы
Предмет: Русский язык,
автор: pozinenko2004
Предмет: Русский язык,
автор: ЕленаИзгагина
Предмет: Английский язык,
автор: dertik314
Предмет: Литература,
автор: natsy0001