Предмет: Алгебра,
автор: tanaselkonogova7
помогите решить пожалуйста
Приложения:
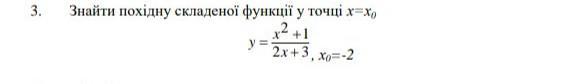
Ответы
Автор ответа:
1
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
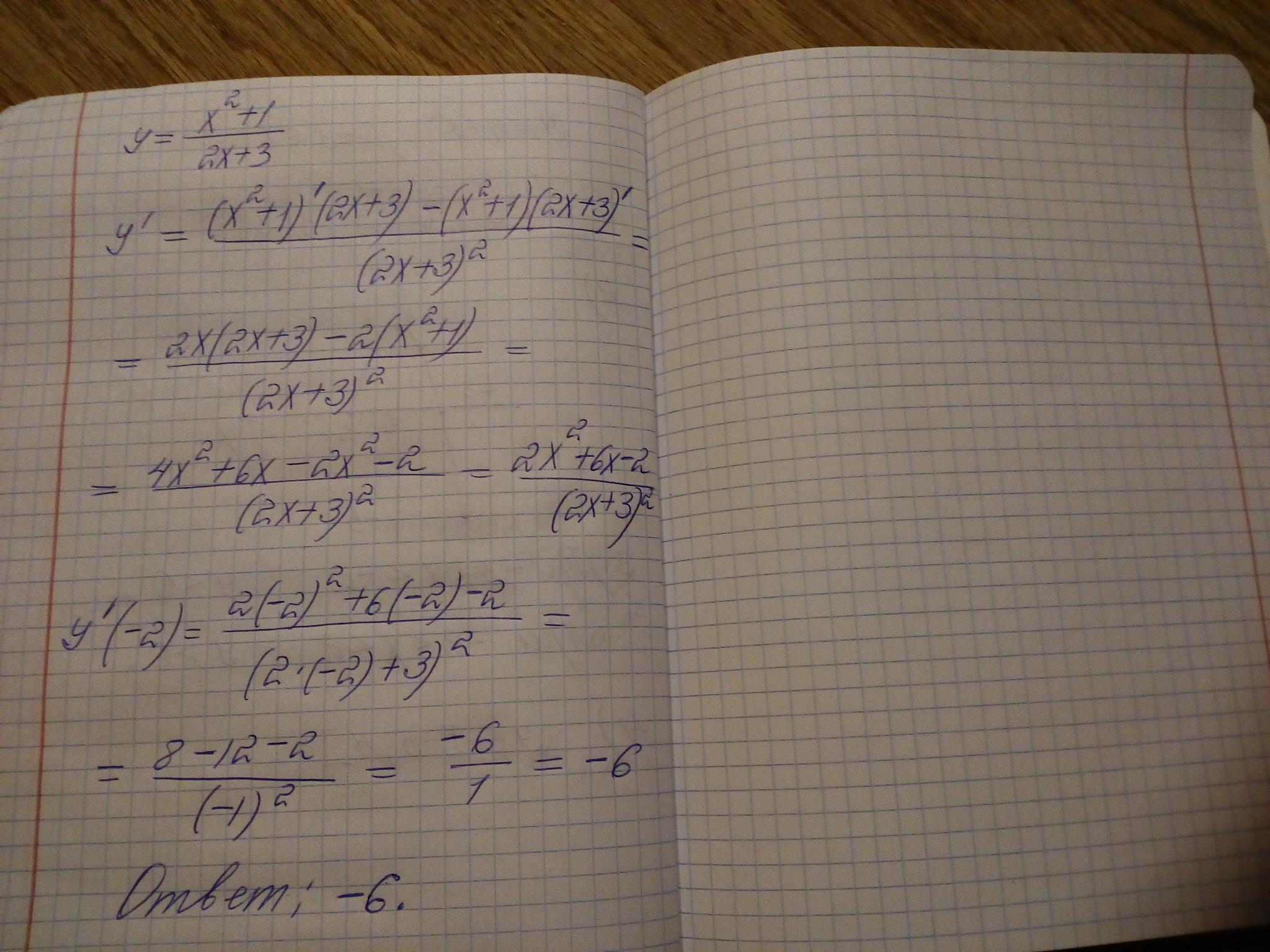
tanaselkonogova7:
можешь решить выше в вопросах ещё 4 задание, пожалуйста
Автор ответа:
1
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: Тока11111
Предмет: Английский язык,
автор: hoki7
Предмет: Английский язык,
автор: лила24
Предмет: Другие предметы,
автор: Kushnirukks
Предмет: Алгебра,
автор: vodila22822