Предмет: Математика,
автор: megagames2145
решите пжжжжжжжжжжжж
Приложения:
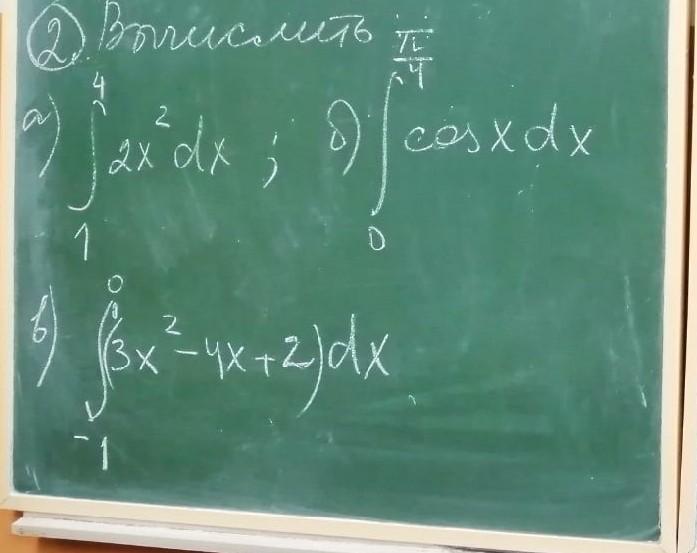
Ответы
Автор ответа:
1
megagames2145:
реши еще одно в профиле пожалуйста
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: erdnigoryaeva25
Предмет: Английский язык,
автор: Leonidos19
Предмет: Английский язык,
автор: markovroma421
Предмет: Английский язык,
автор: PLESENUPLEEEESE